I have a new geometry toy, Tiles. It’s a thing that lets you play with aperiodic tilings, which are special tiles resist tessellating in a way that repeats itself.

You can swap between using kite and dart, and rhombus tiles, which are both kinds of penrose tilings.

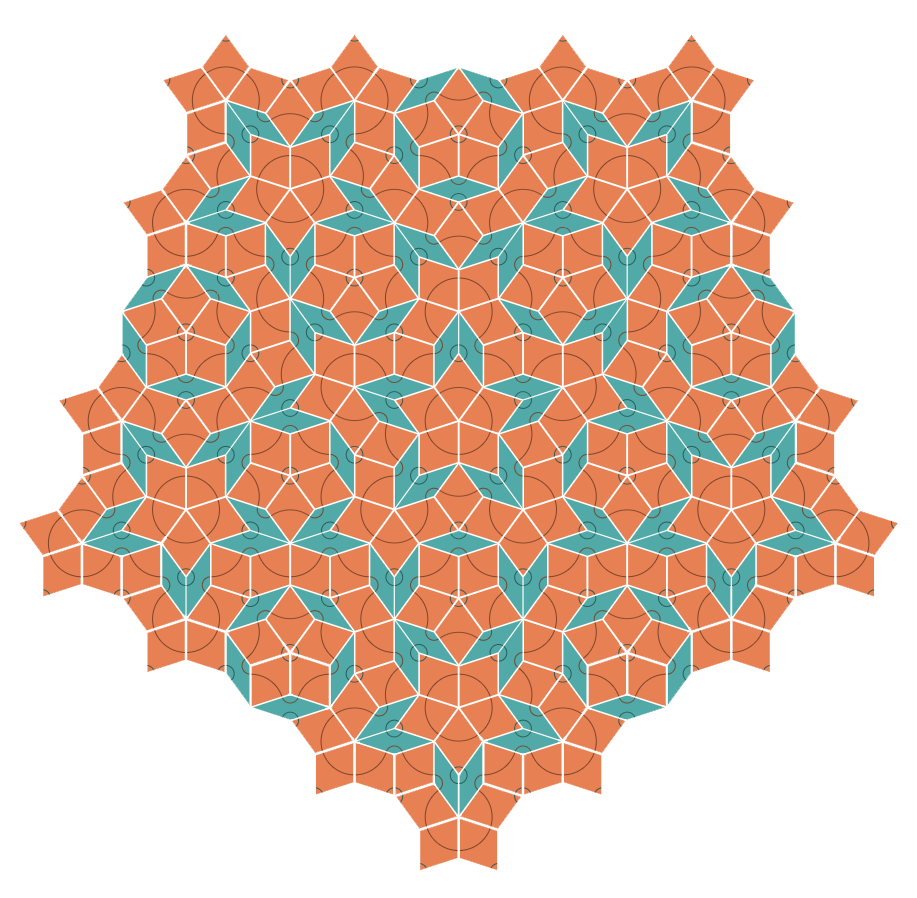I made it just because I wanted to play with these tiles. Originally I was looking for a way to try them out physically, by printing some and cutting them out, but eventually decided that it might be more fun to make it something I could share with other people.

Most my projects start out with me drawing things on paper, and then eventually I move to the computer to try and find an interface that can be used to recreate things I’ve drawn. But with these tiles, I didn’t get to try them out first, so I was far less clear on how it would work then I normally am at the start of my work.

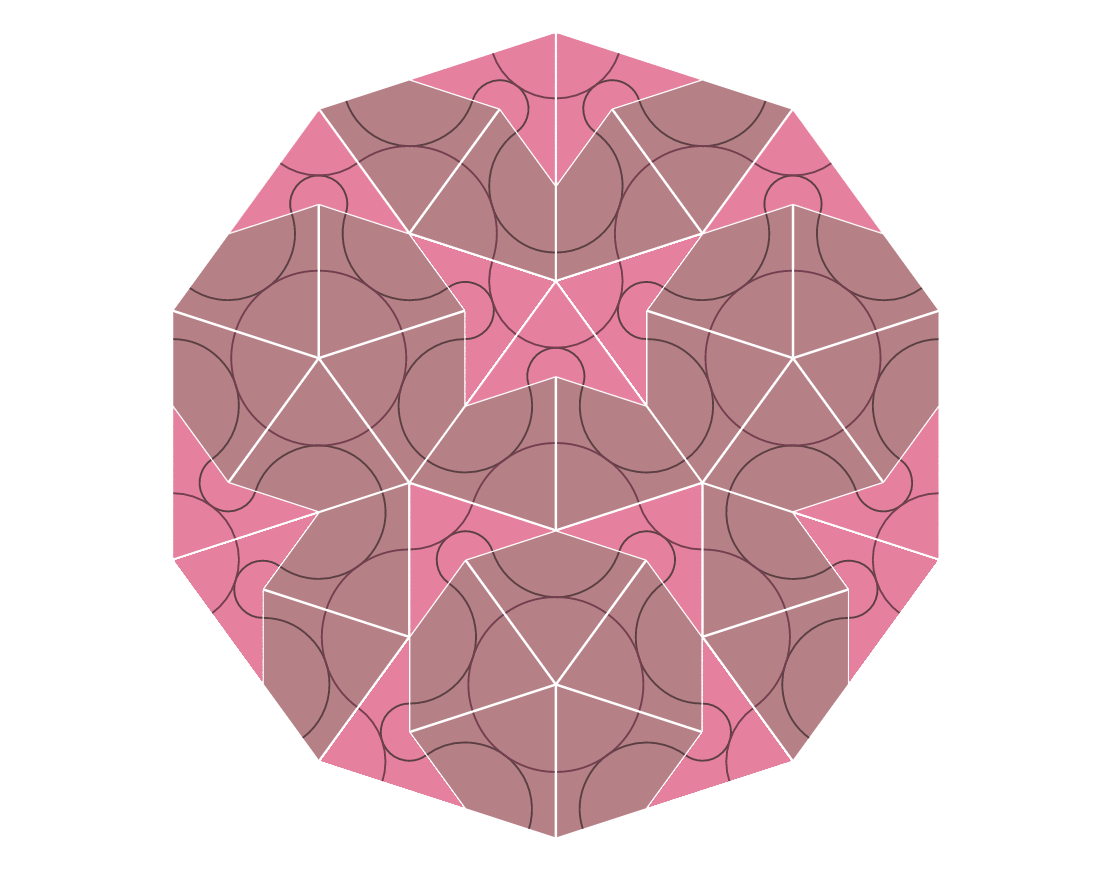The limitations of the tile’s joining rules allowed me to use very simple interface. Only one orientation is allowed for each tile shape per join, so each connection is a binary choice. Sometimes there is only one choice, or no choices, because one or both of the possible tiles would overlap with an existing tile, or a have an edge with an illegal join.

I found that even I’m just clicking around for fun, having limited choices makes placing tiles faster and more playful.

The interface, and lots of the code, is shared directly with Castles Made of Castles. Part of my aim with these two was to make a more modular code base that I could use for sciencevsmagic projects. So in theory it should now be easier to make new ones.

Introducing the Tessellation Kit. It’s a tool that lets you draw tessellations by pushing the edges of shapes into each other.

Just click on the canvas and drag the mouse around to extend a shape, and mathematics will take care of the rest. There a few buttons that let you change the shape of the tiles and the colors you are working with and a toggle for changing how the shape repeats.

Together they make it pretty easy to make something like this:

Despite it’s simplicity, it can do quite a lot. I used it to recreate this Alhambra tiling:

And this interlocking pattern  that Wikipedia tells me is ‘painted porcelain, china’:

The color schemes are generated completely randomly, so I’m sorry if you have to go through a few duds until you find one you like. I quite enjoy the feeling of finding a nice one that’s completely unique, so I didn’t want to just provide a few preset themes, or a simple generator that didn’t provide enough variety.

If you start getting serious, you might want to know that there are a few hotkeys and hidden features:

• ~ or h hide the controls
• z undo
• x redo
• e export to png
• -/+ zoom
• 1-5 operate individual controls.

Today I’m releasing Let’s Play: Ancient Greek Geometry. It’s a Compass and Straightedge tool/puzzle game written in JavaScript. I’ve always thought Geometric Construction felt like a puzzle, so to me this pairing was quite natural. Compass and Straight edge is a technique for constructing shapes out of circles, straight lines, and their intersection points. You can read the wikipedia here – but watch out, some of the gifs are spoilers for the game.

I know that there are a few Compass and Straightedge tools out there already, but none have the simplicity, accessibility or fun of a modern web application, so hopefully mine stands out.

As I said, it’s little bit Geometry tool, and a little bit puzzle game. Throughout development I was conflicted about which was more important. I wanted it to be simple and stripped back enough that you could use this as a go to Compass and Straight edge app, but to make the natural playfulness of geometry to be as visible and as tempting as possible.

In the end I tried to keep the two quite separate. The drawing area is completely free from outside influence, but there is also a  “Challenges” box with achievement style goals. Hopefully this shows off the possibilities of construction and encourages people without getting in the way. If you are the type of person who prefers to make their own goals, you are free to ignore it all together.

Considering this is only my third programming project, and 8 months ago I barely knew what JavaScript was, I’m quite happy with how this project came out. In the next week or two I’m planning to post a few things about how it all works and the technical challenges I faced making it.

I’ve updated the Fractal Machine. It can now skew the motif asymmetrically and add arms that stick out. It also has a new “Auto” mode that dynamically adjusts the settings while the machine animates. Turning Auto on, and pressing H or ~ to hide the controls and pressing F11 for full screen is now officially the best way to watch the Fractal Machine from the couch. The controls have had an overhaul to fit all this new stuff in.

It should also be much faster, and cope much better when drawing a very detailed fractal that requires millions of lines. I’ve heard the old version had crashed a few peoples browsers, this new one shouldn’t do anything like that, even if you tempt fate by turning everything up.

I’ve finished my next project. It’s called the Fractal Machine.

It’s a geometry tool that draws base-motif fractals from five inputs.

If you are unfamiliar with them, fractals are shapes that exhibit self similarity at different scales. This particular type of fractal is created by substituting every line with a shape called the “motif” a number of times.

The Controls

Base changes the base shape the fractal is drawn on. Each side of the polygon will be drawn as one copy of the fractal curve.

Segments cuts the motif into more or fewer pieces of equal length.

Mirror doubles the protruding part of the motif at every level of the fractal.

Depth sets the number of times each line is substituted for the motif.

Angle The slider changes the first and last angles of the motif. Any other angles will sort themselves out to be symmetrical.

EDIT: In June 2013 I added two new controls, Skew and Arms.

Skew Skew the motif left or right.

Arms adds new lines sticking out from the corners of the motif.

The glyphs above show the controls working in isolation (at an angle of 60°), but the fractal machine’s complexity comes from the way in which they interact. Once these inputs are given, the  fractal tries to dynamically resize itself in a way that highlights these relationships. So the length of a single line changes, but the overall size of the fractal and positions of analogous components should be relatively stable. Figuring out the trigonometry that made all this work turned out to be pretty fun.

I figure that some people will want to use this to explore human-scale geometric relationships, while other people will just want to turn on the animation, colors and trails and watch it like a music visualizer. Hopefully most people do a little bit of both and enjoy the way one builds into another. One of my favorite things about recursion is that it can let you see simplicity inside complexity.

If you want the quick tour, some shapes worth checking out include: The famous Koch Snowflake, something I’ve been calling the Koch Mirror, Sierpinski’s Triangle, Sierpinski’s Carpet, this great pentagon fractal, and this cube snowflake I found.

Unfortunately, javascript and canvas are still pretty slow when it comes to a hundred million lines at once, so sometimes the page can get pretty slow. If this gets frustrating, try turning a few of the controls down, depth in particular makes a huge difference.

If you find yourself staring at this for a decent amount of time, you might like to know that you can press H to hide the controls and use the keyboard instead. I’ll leave you to work out what buttons do what.

This has been my second ever programming project (the first being my logic grid/eca), and I’ve learnt a lot. For anyone out there interested in beginning to program, I really recommend JavaScript and canvas as a way to start. Just find a template for an html file with a working canvas, and draw some lines. The rest is actually easier than it looks.

Once I made the logic grid, I figured I may as well make a page that does Elementary Cellular Automata too. It’s at http://sciencevsmagic.net/eca/.

That might actually be more interesting then the logic grid to a lot of you. You can read mathworld about how ECAs work.

I made a cellular automaton in HTML5. I call it the logic grid. Check it out.

It’s basically a maths toy for knitting shapes out of logical rules.

How It Works

• Each intersection is assigned a type based on the input lines coming in from above, the left, and the diagonal upper left. This makes eight possible types, each represented by a diagram in the controls.
• Each type has its own rules about which output lines to draw below, to the right and diagonally to the lower right. These rules can be changed by the user.
• The top left corner is an origin where all three lines are on by default.
• Intersections are only assigned a type after the lines above and to the left have been drawn, so outputs of one row change the types of the next, cascading to infinity.

In pictures:

This is the blank grid after pressing reset. All outputs are off, so the only lines are those of the origin.

I’ve now turned on one output, you can see it in the second diagram in the controls. This one draws a line right from every intersection that has a only diagonal line leading to it. As a result, the origin’s diagonal line now extends one step to the right.

I’ve now turned on a second output that draws a diagonal line from that same type of intersection. However this time, the output of the first intersection has made another of the same type. That one will then make another and so on, so the line now stretches to infinity.

I’ve now added a diagonal output to the intersections that have just a line coming in from the left. After one step an intersection of a new type is created, where lines come in from the left and diagonally. For this type the outputs are off, so unlike the last step these lines don’t continue infinitely.

With one more output, a right line coming out of the new left and diagonal type, everything has gone nuts. Suddenly a whole bunch of complexity has jumped out of the simple rules and made an orderly structure on a much larger scale. This is pretty much just magic.

As far as I know, the method is original, but I wouldn’t be surprised to hear that someone has found these before. There are 8⁸ or 16777216 possible rules, although many of them would be functionally identical (if there are no intersections of a given type, it doesn’t matter what the outputs are) or mirrors of other rules. I have no idea how many unique rules that would leave.

I drew the first one of these with a pencil and some graph paper almost three years ago. Not too long after that I heard about the elementary cellular automata, and saw some similarities. It was only recently when had to rent some server space for another project that I decided to put my extra bandwidth to good use, learn some javascript and finally put it in code.

This is my first real attempt at programming, so things got pretty messy. If you decide to view source feel free to tell me how I’ve done everything wrong in the comments.