Today I’m releasing Let’s Play: Ancient Greek Geometry. It’s a Compass and Straightedge tool/puzzle game written in JavaScript. I’ve always thought Geometric Construction felt like a puzzle, so to me this pairing was quite natural. Compass and Straight edge is a technique for constructing shapes out of circles, straight lines, and their intersection points. You can read the wikipedia here – but watch out, some of the gifs are spoilers for the game.
 I know that there are a few Compass and Straightedge tools out there already, but none have the simplicity, accessibility or fun of a modern web application, so hopefully mine stands out.
I know that there are a few Compass and Straightedge tools out there already, but none have the simplicity, accessibility or fun of a modern web application, so hopefully mine stands out.
As I said, it’s little bit Geometry tool, and a little bit puzzle game. Throughout development I was conflicted about which was more important. I wanted it to be simple and stripped back enough that you could use this as a go to Compass and Straight edge app, but to make the natural playfulness of geometry to be as visible and as tempting as possible.
In the end I tried to keep the two quite separate. The drawing area is completely free from outside influence, but there is also a “Challenges” box with achievement style goals. Hopefully this shows off the possibilities of construction and encourages people without getting in the way. If you are the type of person who prefers to make their own goals, you are free to ignore it all together.
Considering this is only my third programming project, and 8 months ago I barely knew what JavaScript was, I’m quite happy with how this project came out. In the next week or two I’m planning to post a few things about how it all works and the technical challenges I faced making it.
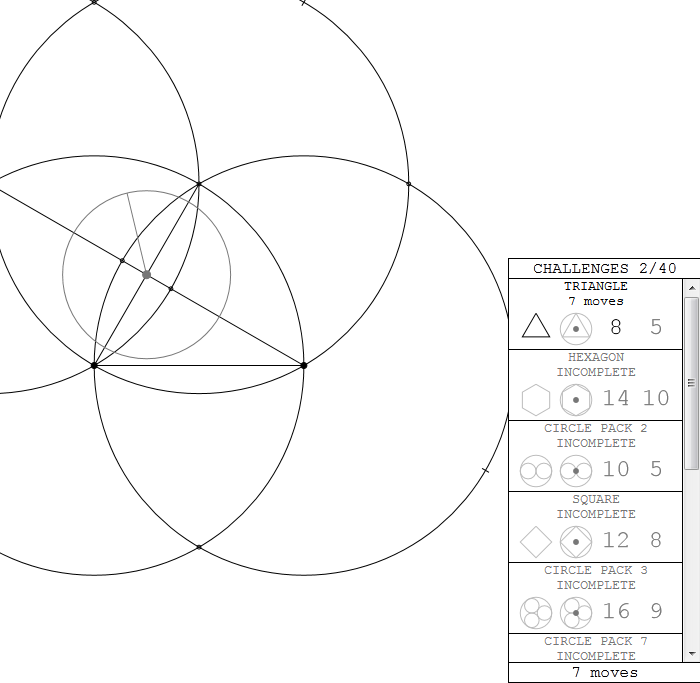
Truly fantastic. We worked through to Circle Pack 3 (in original circle) before getting completely stuck. Tell Geometry its difficulty curve is way off.
Yeah, the lack of control I had over the difficulty curve gave some stress during development. Giving people more things to do when they get stuck on a shape was one of the motivations to add the “in origin circle” and “in X moves” puzzles. And you can always skip ahead and come back later.
SPOILER ALERT
To flatten the difficulty curve, I suggest that you try adding some intermediate constructions as goals. For example, the basic insight you need for the circles-packed-in-the-unit-circle questions is something like this:
http://sciencevsmagic.net/geo/#0A1.1A0.0L1.0A5.5A0.9L10.10A9.9L6.6L10.10L0.0L9.0L6.9A0.31A0.0A29.9L37.0L15.37L60.60A15.N.9L6.6L10.10L9.9L0.0L6.60A15.0A1
draw a polygon around the unit circle, split it into triangles, and then inscribe a triangle in each of those circles.
So would it be possible to add some “inscribe a circle in a triangle” and “draw a polygon around the circle” questions as hints?
The approach I used for the “in origin circle” was to calculate the required diameter of the packed circles and then construct it directly. For example Circle Pack 3 can be done like this: http://www.sciencevsmagic.net/geo/#0A1.1A0.0L1.2L3.0L4.1L5.4A2.8A4.5L11.5A11.1A16.16A5.2L1.1L3.32A2.38A3. By the way the spoilers don’t line-wrap so they go right off the page when shown.
I did it this way. Using a less magic approach of creating the 3 in a circle then scaling it using parallel lines. I have reasoning for every step of the process:
https://sciencevsmagic.net/geo/#1A0.0A1.3L2.0L1.3A4.2A4.1L5.5L3.5L2.5A17.1A24.1L2.2L30.1L19.19L43.1L29.5L24.0L33.1L40.2L43.5L43.5L40.3L40.3L33.2L33.N.1A0.41A19.90A41.98A90.41L104.88A41.139A88.41L148.104L117.117A5.148L164.164A2.38A190.226A38.239A226.38L249.249L259.259A3.N.1A0.259A3.117A5.164A2
why is this not accept my center point http://www.sciencevsmagic.net/geo/#0A1.1A0.2L3.0L1.0L5.2L5.3L5.5A0.2A0.3A0.0L7.3A4.5A24.2A4.0A42
also this one as well what is the origin center point if this isn’t
http://www.sciencevsmagic.net/geo/#0A1.0L1.1A0.1L5.5A1.7A1.4A0.6A1.3A0.0L2.5L8.1L6.6L16.1L3.3L18.1L4.4L15.1L7.7L17.16A6.8A5.17A7.15A4.2A0.18A3.1A19
For all the “in origin circle” puzzles, the shape must be in a circle with one starting point at its center and the other at its edge. Like this: http://www.sciencevsmagic.net/geo/#1A0.0A1.3A0.0L4.2A0.0L8.2L3.13A0.12A0.0A12.13L27.0L1.42A0.N.42A0.1A42.1L4.1L3.1L8.1L43.1L2.1A50.79A3.75A4.72A43.78A8.71A2.1A0.N.1A50.72A43.75A4.79A3.42A0.71A2.78A8.1A0
This is pure brilliance. I am hooked. Thank you. Now to attack the final 7 challenges!
Can you confirm that all the challenges are possible in the lower number of moves? The square seems particularly doubtful in 8 moves. Also “circle pack 7” is possible in 13, if the lower numbers are meant to be minimal.
I assure you they are all possible.
If you need a hint I will tell you that the 8 move square is also an “in origin circle” solution. And don’t forget that extending existing lines is “free”.
As for the circle pack 7, the minimal scores were just the best I found during development. I was hoping that someone would be able to surprise me with a better one and I haven’t been disappointed. Maybe I should go back and change it now there is a new record, but I think it’s kind of fun for people for people to know when they have bested me.
Got them all, now can sleep. Will be using this in teaching soon.
What other minimal scores have been beaten?
Congratulations!
So far I only know of the circle pack 7. I hope more start to show up though.
I would love to hear how it goes in teaching, its really exciting that the game encourages people to engage with mathematics in a different way than usual.
I found a 14 move pentagon
[SPOILERS] http://sciencevsmagic.net/geo/#0A1.1A0.0L1.2L3.6A0.8A6.3L15.15L1.15A8.15L28.1A28.2L34.0L30.30L34.0A34.49L1.49L34
I tried to make a real 17-gon too, not sure what went wrong. I improved yours to 65 moves though:
I have beaten the minimum goals of both the pentagon and dodecagon. I got the pentagon in 12 moves and the dodecagon in 18. the dodecagon I did via http://sciencevsmagic.net/geo/#0A1.1A0.3L2.2A0.2L7.6A2.4L11.11L0.0L6.6L1.1L10.10L5.7A2.4L37.5L38.38L48.37L44.48L37.44L38.55L7.7L61
and the pentagon as
http://sciencevsmagic.net/geo/#0A1.0L1.0L2.2A0.1A2.6L3.0A9.12L9.9L18.9A18.12L27.27L26.26L13.13L9
I still have not figured out origin circle pack 3 and pack 4. The rest I have.
Thanks, really enjoying this. The square-in-8 one is driving me nuts too, though I’m only at 30/40 so plenty left really.
Well at 40/40, but still haven’t hit the minimum moves on 5. Any way you can link to an “official” place to discuss these with spoilers? I don’t want to pollute this space with details.
I think I have spoiler tags installed.
Use [spoil*er] and [/spoil*er] without the *s to use them.
Well, there is a bug somewhere.
Well that didn’t work.
Sorry, I meant [spoil*er] without the s. I’ve edited out comments to fix them.
Sorry about the bug. I can’t make any promises about the behavior of the Easter egg polygons.
Can’t nest deeper so responding here.
Thanks! That looks like the same construction I used, so I probably just made a mistake. Other than them occasionally disappearing from the list, everything works great. Thanks for checking for me!
Finally got the minimum number of moves for the square, octagon, and circle pack 4! Thanks again for making this.
Loving this little piece of programming!
Still 12 challenges to go but it has been pretty damn fun already. brings back some geometry q n a’s 😉
keep up the nice work on this site!
Nico, this work is amazing! It is elegant and simple to use. I have always meant to try my hand at this sort of geometry and this was a challenging and fun way to do it. I did have to get some hints for the pentagons, but I discovered the pack 3 circles through just messing about. Brilliant!
It would be nice to have the numbers counted separately for the construction vs in-original-circle. Otherwise you can construct something in the minimum steps and then take hundreds of steps to do the in-original-circle ones and your scoreboard looks the same at first glance.
You could also add exscribed figure challenges as these are simple to understand but present a different (harder?) challenge.
Thanks again for this wonderful tool/toy. May everything you make be this good.
Am I missing something? I don’t seem to be able to draw lines that go _through_ a point.
E.g.
http://sciencevsmagic.net/geo/#0A1.1A0.0L1
the points are the end points but I want that line to extend and intersect the circle. Is there something non-ancient-greek about that?
Aha, drag the end-point afterwards.
BTW you might also want to add a compass-only set of problems.
Wow, this is absolutely fantastic. I have nothing really to say, just needed to express my appreciation. The smoothness of this tool is amazing, and it’s a delight to use. Only 17 done so far, but I’m still plowing through!
This is an awesome app. Shelley introduced me to it, and I’ve been trying to optimize existing shapes as well as make good approximations to unconstructable ones. Just now I actually got it to recognize a regular 7-gon!
Weird! and well done!
You’ve exposed the tolerance in my code. I need some because javascript’s rounds off all my numbers – nothing ends up being perfect. But here it’s causing problems. Perhaps I should make it a bit stricter.
9-gon works too:
Hah, nice one. Not sure what you did there, but it’s cool. I also have a 9-gon:
And a fake 17-gon:
I was playing around with the 7-gon solution above and was able to reduce it to 22 moves and place it in the origin circle.
How the square in 8 or less moves is done? Are you sure this is possible, nico? I cannot even do less than 9 using the “in original circle” method.
It is definitely possible. I’ll give you another clue:
and if you are still stuck:
There’s something strange about that spoiler.
Whoops. I’ve fixed it now. Thanks.
But
I’m definitely stuck on this challenge. There must be some obscure gimmicks that I didn’t know.
As Pitarou pointed out, I got one of my clues wrong. It’s fixed now.
Hey, fantastic work. I’m trying to get Challenge Pack 4 in 12 moves, and I thought I had it, but it seems I’m having some difficulty – a point should be clickable and it’s not, and I think it might be a bug?
I’m assuming there’s some other way. One way or another, any help / hints appreciated.
How many moves do you have for circle pack 3 in origin circle? I have it down to 15 but it looks so ugly that I’m holding out for a cleaner solution.
My bests for in-origin circle problems are as follows:
triangle: 6
hexagon: 14
circle pack 2: 9
square: 8
circle pack 3: 15
circle pack 7: 15
octagon: 15
dodecagon: 22
circle pack 4: 18
pentagon: 16
Some improvements I have:
hexagon in origin circle: 10
circle pack 2 in origin circle: 7
circle pack 3 in origin circle: 13
dodecagon in origin circle: 20
circle pack 4 in origin circle: 13
Circle pack 3 in origin circle: 10 moves
Pentagon in origin circle: 15 moves
Pentagon in origin circle: 14 moves
Wow, I didn’t think a pentagon in origin circle could be done under 15. Great job!
Pentagon in origin circle: 13 moves ! 😀
Pentagon in origin circle: 11 moves. 🙂
11 moves, wat? Can I have a hint?
Sure: the important insight was that, if you imagine extending the pentagon’s sides into a star, then constructing a point of the star allows you to draw two sides of the pentagon without finding all of its vertices beforehand.
Meanwhile, I just found
Dodecagon: 17 moves
Dodecagon in origin circle: 18 moves
Hexagon in origin circle: 9 moves
Octagon in origin circle: 14 moves
Dodecagon in origin circle: 17 moves
Circle pack 4 in origin circle: 12 moves
Whats your hint for dodecagon in 17?
A hint for hexagon in 9, octagon in 14, and dodecagon in 17:
I’m still stuck on pentagon in 11 though :p
It’s based on the same trick with stars—that’s enough to get you 18 without much trouble. But there are multiple ways to extend the sides of a dodecagon to a star, and one of them has a beautiful coincidence with the circles you’ve already drawn.
After I posted that last night I ended up finding the 18 on my own! Star based construction definitely seems to be the way to go.
There’s an appealing symmetry to this 14-move Pentagon in origin circle:
http://sciencevsmagic.net/geo/#0A1.1A0.2A0.5L0.0L7.6A0.8L9.13A3.22A0.26L6.6L27.23A0.26L56.56L55.55L27%5B/spoiler%5D
Hmm … 11 eh ?
I was just re-running my brute force pentagon in origin circle (22ish), after getting a plain pentagon down to 15, when I noticed a coincidence; when I’d worked out why that happened, and noticed a second coincidence (one of my early construction lines just happened to pass through two points I was doing a lot of work to construct), I found I could get rid of lots. Even so, I was pleasantly surprised to get down to 12. So … 11 eh ?
Just when I thought I could, satisfied, put this toy on one side …
Circle pack 7 in origin circle: 14 moves
circle 7 can be done in 13. Not in origin tho.
http://www.sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A1.0A5.0L2.2L14.0L13.0L11.0L3.3L17.0L16.14A2.16A15.11A4.13A12.17A3.0A8
Yeah, that was reported by Edmund Harriss last week (http://blog.sciencevsmagic.net/science/lets-play-ancient-greek-geometry/#comment-71).
I have managed a 14 move pentagon http://sciencevsmagic.net/geo/#0A1.1L0.1A2.2A3.3A2.5L6.9L0.0L12.9A10.18L17.9A11.32L8.8L33.33L18.17L32
How to construct a octagon in 15 moves? My best attempt is 17 moves:
http://www.sciencevsmagic.net/geo/#0A1.1A0.2L0.0L4.2L1.1L5.5L4.3L2.4L1.0L5.6A0.0L1.11A0.14A6.N.11A0.6A0.14A6.2L4.4L5.5L2
geometry for the lols
ILLUMINATI
A really wonderful webpage. Two suggestions: I’d like to be able to create a random point, rather than construct it, and I’d like to be able to copy a length from one place to the other, although I’m not sure how that would be implemented nicely.
Being able to just copy a length would be outside of the bounds of traditional compass and straight edge, because it requires a “sticky” compass.
You can copy a length with a sequence of straight edge and compass moves, but it would change the nature of the game to make this a separate operation.
I’m absolutely loving this! Lots of fun.
However, I think I’ve solved the circle pack 4 but my solution isn’t being recognized.
http://sciencevsmagic.net/geo/#1A0.1L0.1L2.2A0.0A2.5L4.8L0.0L7.7L2.2L8.0A7.7A0.27L1.N.7A31.0A31.8A32.2A32.1L86.1A42
Hi Emily,
You got pretty close, but you didn’t quite draw the final circle big enough. If you zoom in on the point(s) where the big circle touches a little circle, you’ll see why/how you missed it. Undo and draw just the last circle again, watching the dots at the intersections very carefully.
Yep! Thanks! I had the right idea, it just snapped to the wrong point at the last second. Got it now.
Your very last circle is slightly wrong; it’s very close to, but not quite, tangent to the other four. It will work if you undo once and redraw it carefully.
Could anyone check my solution for the 2 packed circles, it doesnt get recognized… http://sciencevsmagic.net/geo/#0L1.0A1.1A0.1L2.0A5.2A0
Great game! But I think it’s not recognizing all of my correct solutions. E.g., this one should count for circle pack 7 around the origin circle, right?
http://www.sciencevsmagic.net/geo/#0A1.1A0.2A0.4A0.6A0.6L4.4L2.2L1.1L3.3L8.8L6.0L7.4A13.2A13.6A23.1A34.8A14.3A14.6L0.0A64.0A63
Or am I doing something wrong?
It needs to be within the origin circle, not just around it. Confused me at first, too.
I believe this should give me Circle Pack 4 in 12 moves, but it doesn’t seem to recognise it:
http://www.sciencevsmagic.net/geo/#0A1.1L0.0L2.2A1.1A2.0L4.8A7.7A8.N.4A16.13A10.5A10.14A11.4L26.0A26
Ah my mistake – I can see that the circles don’t quite connect to each other on the inside. They intersect or whatever.
In 9 days, you’ve gotten quite a following already. I don’t remember who mentioned this first, but when it got mentioned again, and I got some help with the interface, I began to love it. I blogged about it here.
It’s lovely, but one of them leaves me puzzled – I’d _swear_ I have the square in circle just right, but it’s not recognizing it at all?
http://sciencevsmagic.net/geo/#0L1.0A1.1A0.3L4.6A3.0L2.1L5.3L7.7L4.4L8.8L3
The circle that it has to be in is the first circle you make. Not just any circle.
Sorry, I’m afraid magic wins:
http://sciencevsmagic.net/geo/#1A0.0A1.3L2.0L1.4A5.5A4.6A4.4A15.15A4.22A4.4A33.33A4.42A4.4A55.55A4.66A4.4A81.81A4.94A4.4A111.111A4.126A4.4A145.145A4.162A4.4A183.183A4.202A4.4A223.223A4.242A4.4A263.263A4.4A303.282A4.303A4.306A4.4A345.345A4.4A389.366A4.389A4.392A4.4A435.435A4.458A4.4A483.483L506.482L505
Accidentally made one when trying to optimize a nonagon.
http://www.sciencevsmagic.net/geo/#1A0.0L1.1L2.2A0.0A2.5L4.7A1.9L10.10L18.2A1.2L25.25L31.7A16.25A29.37L47.47L49.1L25.2A57.57L64.1L79.79L96.2L92.1L106.N.1A0.2A121.121A2.142A121.21A142.184A21.198A204.206A198.210A207.218A210.2L142.142L184.184L206.206L218.210L231.231L348.348L2.198L215.215L392.392L348.21L200.200L433.392L433.142L193.193L469
wow i just made a 48-gon in 94 moves now working on a 96-gon 🙂 way to close lines ftw
http://blog.sciencevsmagic.net/science/lets-play-ancient-greek-geometry/#comment-140 here’s the link of my 48-gon
okey i could have done it in way less moves 🙁
Yes indeed.
10-gon: 16 moves
15-gon: 22 moves
16-gon: 23 moves
17-gon: 40 moves
20-gon: 29 moves
24-gon: 30 moves
30-gon: 38 moves
32-gon: 41 moves
34-gon: 57 moves
40-gon: 49 moves
48-gon: 56 moves
Hmm. Hey nicomallo, maybe it’s time for a high score board? 🙂
(Those were all in origin circle, by the way.)
30-gon in origin circle: 37 moves
32-gon in origin circle: 40 moves
http://www.sciencevsmagic.net/geo/#0A1.1A0.2A0.4A0.6A0.8A0.3A0.0L10.9L0.0L7.0L5.0L12.0L11.14A0.16A0.17A0.13A0.18A0.15A0.0L59.0L44.0L50.0L27.0L47.0L33.0L30.0L24.0L36.0L62.0L21.0L53.73A0.75A0.77A0.71A0.69A0.67A0.78A0.76A0.72A0.74A0.70A0.68A0.0L253.0L98.0L228.0L125.0L236.0L267.0L183.0L257.0L210.0L222.0L175.0L242.0L149.0L204.0L139.0L188.0L84.0L169.0L105.0L160.0L120.0L134.0L273.0L89.294A0.292A0.290A0.288A0.286A0.305A0.295A0.301A0.284A0.303A0.297A0.299A0.293A0.291A0.289A0.285A0.287A0.283A0.306A0.304A0.302A0.298A0.300A0.296A0.553L0.0L873.917L0.847L0.0L815.631L0.0L769.0L486.0L756.438L0.0L404.708L0.0L570.352L0.0L588.320L0.0L683.0L1101.0L518.0L1074.0L648.0L1121.0L471.0L1054.0L451.0L399.0L992.0L367.0L1011.0L937.0L312.0L890.0L1107.913L0.0L1068.857L0.0L1135.801L0.1035L0.786L0.0L1016.740L0.0L671.525L0.1191L73.73L1156.1156L295.295L1157.1157L6.6L1160.1160L301.301L1162.1162L75.75L1164.1164L303.303L1165.1165L15.15L1169.1169L305.305L1168.1168L77.77L1172.1172L284.284L1173.1173L4.4L1176.1176L286.286L1177.1177L68.68L1180.1180L288.288L1182.1182L18.18L1184.1184L290.290L1186.1186L70.70L1188.1188L292.292L1148.1148L2.2L1149.1149L294.294L1190.1190L72.1152L300.72L1152.300L1194.1194L13.13L1154.1154L298.298L1192.1192L74.74L1155.1155L296.296L5281.296L1158.1158L1.1L1159.1159L302.302L1161.1161L76.1163L76.1163L304.304L1166.1166L16.16L1170.1170L306.306L1167.1167L78.78L1171.1171L283.283L1174.1174L3.3L1175.0L948.0L604.976L0.716L0.1175L285.285L1178.1178L67.67L1179.1179L287.287L1181.1181L17.17L1183.1183L289.289L1185.1185L69.69L1187.1187L291.291L1147.1147L8.8L1150.1150L293.293L1189.1189L71.71L1151.1151L299.299L1193.1193L14.14L1153.1153L297.297L1191 i hope your pc can handle it 96-gon
why doesn’t this count as a octagon?http://www.sciencevsmagic.net/geo/#0A1.1A0.0L1.3L2.6A0.2A6.3A6.6L9.6L12.6L18.17L6.0L29.29L7.7L25.25L1.1L30.30L8.8L26.26L0
Because it isn’t a regular octogon? The diagonals do not bisect the right angles.
You drew the last two circles (the two centered on the vertical axis) incorrectly. They should use the diagonal of the center circle as a radius. They way they are drawn, they are using the endpoints of the vertical line segment as centers and are tangent to each other at the center of the octagon.
thanks blaise i fixed it 🙂
what exactly are the paramiters for “in origin circle” as this is the first time i have even touched geometry on this level i don’t understand therefore cannot complete the goals
After you hit “reset” there are two points, and there are three things you can do: make a line between the two points, or create one of two circles, each centered on one of the points and passing through the other.
Either of those two possible original circles works as an “origin” circle. I suspect, without testing, that any circle who’s radius is the same as the distance between the first two points would also count.
i’m having the same problem though the middle point of my first circle is the middle of my 3-circle still it doesn’t recognizes it as an in origin circle awnser http://www.sciencevsmagic.net/geo/#0A1.1A0.1L0.0L4.2L3.3L4.2A6.3A6.4A18.0A23
You have a centered 3-packed circles, but the circles are packed within an “origin circle”.
Imagine the circle you get in step 1 as “given”, and put the 3-packed circles within it. Then you’ll get it.
Here’s a 3-packed circles in origin circle done in 17 moves. I don’t claim it’s optimal, but it shows what “in origin circle” means in this case.
I’m having a hard time with something. After creating the 9-move 3-pack (http://sciencevsmagic.net/geo/#0A1.1A0.3A0.5A1.6A1.7A3.1L7.3L6.16A15), I want to create the triangle whose vertices are the points where the packed circles are tangent to the outer circle. Those points should already be created (right? basic construction: create the one or two points where two circles intersect), but I can’t seem to select them.
Now, obviously, I can pin down those points with lines (two of them with lines that already exist), but I don’t think I should have to. Am I just misunderstanding what’s possible?
how do you make the sqaure in 8 turns i feal so stupid right now 🙁
A previous hint said it was (a) inside an origin circle, (b) was done with three circles and (c) five lines. I’ll go farther by saying that the three circles are all the same size, and can be made before any lines are made.
The first line I drew I needed to extend, but extending a line is a free act (the Euclidean postulates say that a line goes through two points, not that a line segment is terminated by two points).
Is that enough to help?
oh god thank you i finnaly finished it http://www.sciencevsmagic.net/geo/#1A0.0A1.3A0.2L3.3L7.7L5.5L6.6L4.4L7
That answers one question I had… does it count as being in the origin circle if it isn’t in a unit circle centered on one of the first two points? And the answer is no.
Believe it or not, this is not the square-in-8 I was thinking of. I was thinking of a different square-in-8 that also counts as in the origin circle. If you draw the first line 120 degrees rotated from where you did, the square will end up in the origin circle.
120 degrees? how?
I see it now 🙂
Ideas/pleas for version 2…
Have a way to erase lines. Once I’ve bisected a line, I’d like to remove the circles I needed to get there.
Add extra dots before starting. (For the puzzle – Starting from three dots, draw a circle that goes through all three dots.)
… i just made a 2-gon http://sciencevsmagic.net/geo/#1A0.0A1.3L2.0L1.4A5.5A4.6A4.4A15.15A4.22A4.4A33.33A4.42A4.4A55.55A4.66A4.4A81.81A4.94A4.4A111.111A4.126A4.4A145.145A4.162A4.4A183.183A4.202A4.4A223.223A4.242A4.4A263.263A4.4A303.282A4.303A4.306A4.4A345.345A4.4A389.366A4.389A4.392A4.4A435.435A4.458A4.4A483.483L506.482L505.482L793
Hahaha, well done.
My app assumes that two line segments with sufficiently similar angles are supposed to be same and it’s 64-bit floating point numbers that are to blame for the discrepancy. (with maybe a little too much tolerance). So here your four line shape is treated as though it’s a two line one.
minimum moves for 2-gon http://www.sciencevsmagic.net/geo/#1A0.0A1.3L2.0L1.4A5.5A4.6A4.4A15.15A4.22A4.4A33.33A4.42A4.4A55.55A4.66A4.4A81.81A4.94A4.4A111.111A4.126A4.4A145.145A4.162A4.4A183.183A4.202A4.4A223.223A4.242A4.4A263.282L263.262L281
Nope.
http://www.sciencevsmagic.net/geo/#0A1.1A0.1L0.0L4.1L5.4A5.5A4.4L6.5L9.6A9.9A6.4L2.2L20.4L17.7L0.0L28.11A28.12L7.7L41.41A40.41L52.52A40.52L63.63A40.63L74.66L74.66A87.92L74.90L74
Actually tried this time.
Haven’t been able to get less for an hour.
http://www.sciencevsmagic.net/geo/#0L1.1A0.1L2.2A0.2L3.3A0.3L4.4A0.4L5.0A5.0L6.0A1.12A0.12L11.33L6.33L38.5L33
sorry this is the minimum 42 moves for 2-gon http://www.sciencevsmagic.net/geo/#1A0.0A1.3L2.0L1.4A5.5A4.6A4.4A15.15A4.22A4.4A33.33A4.42A4.4A55.55A4.66A4.4A81.81A4.94A4.4A111.111A4.126A4.4A145.145A4.162A4.4A183.183A4.202A4.4A223.223A4.242A4.4A263.263A4.4A303.282A4.303L306.324L302
What is a 2-gon? If it’s what I think it is, why isn’t a 1-move solution possible?
i don’t know what it is… it just happened
My app assumes that two line segments with sufficiently similar angles are supposed to be same and it’s 64-bit floating point numbers that are to blame for the discrepancy. (with maybe a little too much tolerance). So here a four line shape is treated as though it’s a two line one.
Nope.
http://www.sciencevsmagic.net/geo/#0A1.1A0.1L0.0L4.1L5.4A5.5A4.4L6.5L9.6A9.9A6.4L2.2L20.4L17.7L0.0L28.11A28.12L7.7L41.41A40.41L52.52A40.52L63.63A40.63L74.66L74.66A87.92L74.90L74
Actually tried this time.
Haven’t been able to get less for an hour.
http://www.sciencevsmagic.net/geo/#0L1.1A0.1L2.2A0.2L3.3A0.3L4.4A0.4L5.0A5.0L6.0A1.12A0.12L11.33L6.33L38.5L33
It doesn’t seem to recognise either http://www.sciencevsmagic.net/geo/#0A1.1A0.2L1.1L3.2A0.6A0.8A0.3A0.9A0.2L6.6L8.8L9.9L3.0L10.0L7.0L5.0L4.0L11.0L12.8A14.6A14.2A17.1A13.3A13.9A18.0L1.0A76.1L78.0A75 or http://www.sciencevsmagic.net/geo/#1A0.0A1.3A0.4A1.6A1.8A1.2A0.3L0.0L2.2L8.8L6.6L4.4L3.5L1.1L11.1L12.1L10.1L9.1L7.3A13.4A18.6A14.8A14.2A17.0A13.1L0.1A76.1L73.1L74.1L4.4L100.1L2.2L101.1L3.3L105.105L106.1A75 as origin-circle circle pack 7s. Is this correct?
That is correct. Neither 7-pack is within the origin circle.
how does one do a pentagon in 11 moves my pentagon record is 14 moves
Brilliant!
I was bored so I drew you guys a circle the size of the known universe (well, 60% larger because I’m generous)… assume that the smallest circle (between the 2 origin points) is the size of a gold atom’s nucleus (8.45 femtometres).
http://tinyurl.com/lxlgrut (link is obnoxiously large without tinyurl shortening)
wow I couldn’t reach the start
pokeball lololol http://www.sciencevsmagic.net/geo/#1A0.0L1.1L2.2A1.4L3.1A6.6A1.11L10.1A14.N.1A14.0L23.14L2.1A0.14A1.25L24.1A28.N.1A28.1A14.1A0.0L23.14L2
smallest circle possible http://www.sciencevsmagic.net/geo/#1A0.0A1.3L2.1L0.4A0.1A4.12L11.4A14.14A1.25L24.4A28.28A4.45L44.4A48.48A4.67L66.4A70.70A4.91L90.4A94.94A4.113L112.4A116.116A4.137L136.4A140.140A4.4L140.N.4A140.4A116.4A94.4A70.4A48.4A28.4A14.4A0.4A138.4A114.4A92.4A68.4A26.4A46
dear nicomallo you should make a app out off this for iPad and playstore i would love to play this in the train without bringing my dad’s laptop i think that you would really benefit of the touch screen you could zoom in and out by either using two fingers going up for zooming in and down for zooming out
The page has touch controls and works fine of the iPad I used for testing (although I’m not sure if it works on older ones). You should be able to save the page to your home screen if you want to use it like an app.
Try it out and let me know what you think.
just played it on my iPad4 i think it’s awesome i didn’t really expect it to work but it does it can be a little laggy but everything ells works awesome
This is awesome! I’ve wasted more time here than I care to think about.
One note: It would be nice to have a “center” function. I managed to trip over my trackpad, and zoom my image down really small then sweep it off the visible screen, and after that could not get it to reappear in my view again. This was especially annoying as I was working on the pentagon!
But I’m impressed if this is only your third program. Kudos, I’ve been enjoying it quite a bit!
Thanks.
Refreshing the page will center your construction.
http://sciencevsmagic.net/geo/#0A1.1A0.2A3.4A0.0A5
Why is this no valid solution for circle pack 2 with 5 moves?
It registers fine for me.
Perhaps you have already solved it in 5 moves. The shape will only go dark if you create an improved solution (fewer moves for either the default or in origin solution). This is to avoid having shapes go dark all over the place whenever you retrace your steps.
If you want to double check a solution that is no better then one you have, use a private browsing window so it is in a different browser session.
Ah ok, I did this solution on first try 🙂
I have a similiar problem. I have this solution: http://sciencevsmagic.net/geo/#0A1.1A0.0L1.0L4.4A0.0A5 on the first try. It did register that I solved it in 5 moves, but not that I solved it in origin circle. Am I missing something?
Nvm, the origin circle seems to be the first circle that I draw and not a circle that has one of the two starting points as it’s centre. My mistake.
Nico,
Have you watched any video’s by Scott Onstott? Check out his youtube channel!
Hi!
Great game. Is there any way to save drawings made on this?
copy and paste the link to a text program like word if you click the link your drawing is opened
First of all, fantastic job! The app is really nice. I absolutely love the “challenge” aspect. A few ideas —
-Maybe keep a list on the site somewhere of solutions people have found, including the ones in the fewest number of moves?
-Maybe include some way for people to make (and maybe post) their own challenges?
-It would not be too difficult to write a program to search for minimal solutions to the problems; perhaps you could use this to generate “minimal move” targets/give people some way to know they’ve found a solution with as few moves as possible?
-Maybe also include some tool that can measure angles and lengths (assuming the distance between the first two points is 1) so people can check to make sure they’ve constructed what they think they have (of course this couldn’t be used to actually construct anything, it would just be a self-check tool).
I dunno if you plan to do any more with this but I think these changes would be really cool!
Thanks Max,
I would love it if people could create their own challenges. Maybe if I create a version 2 one day….
A bot that looks for minimal solutions sounds great, my source is available in the page, so anyone could write one.
As is my app isn’t clever enough to know the exact values of lines in relation to the starting line. It just uses floating point values, so I think a ruler would be a bit of a disappointment.
Is there a good definition of “in origin circle?” What defines the “origin circle?” I’ve managed to do some of the constructions centered about one of the two original points but that doesn’t seem to satisfy the “in origin circle.” Is the origin circle the circle defined with the center at one of the points and having the other point on its circumference?
Definitely fun though!
circle 7-pack in 13 moves:
[SPOILER]test[/SPOILER]
oops, let’s try that again.
The origin circle is the first circle you create, so far as I can tell.
So it seems. 🙂 Thx, this helped me progres
Circle pack 5. not in origin circle though.
Great fun. Does this get recognised.
Circle pack 7 in 13 moves:
Beat all the challenges, but my save reset. Oh well, glad it happened now.
For anyone who has done all the secret challenges and wants another one, try the Nepali flag. It has a geometric construction defined on its wiki page, and doesn’t seem too hard to do.
http://en.wikipedia.org/wiki/Flag_of_Nepal#Flag_layout
What is the meaning of the two numbers on the right of each challenge? The right most one seems to be the minimum number of moves. What about the left one?
It’s just an easier goal for people who are just starting to optimize. I put in numbers that I thought would be relatively obtainable.
The right most number was my lowest number of moves as of release, but lots of them have since been beaten, some by quite a bit.
If I make a version 2 I’ll probably use the new best minimums.
It is not working when I use Google Chrome. Is this expected? How can I solve this problem?
About 15 hours and: CHALLENGES 40/40
Thank you for this puzzlers!
There is 44 challenges though!
I completed all tasks, both levels, but still got only 37/40 points :o(. Any ideas why?
I haven’t heard of that problem before. Perhaps double check that you have all four challenges solved on each shape.
This has got to be the best game I have ever played. I feel like it was designed just for me.
It took a few weeks, but I have completed all the challenges.
Please, please, won’t you add some more?
Thank you!
Sincerely,
Erik Mulet
Thanks so much Erik. I thought I was designing it just for me, but I guess there are quite a few of us.
If you like you can create regular polygons that aren’t listed (like a decagon) and they will pop in, so it’s possible to get more then 40 points.
Many shapes can be made in fewer moves then my challenges, try looking through the comments here for other people’s scores and try to match them.
If you have any ideas for a whole new kind of challenge, let me know. I’m open to the idea of adding some more, but only if they make sense among the others.
Well done!!! 🙂
Here’s an octagon in 13:
http://sciencevsmagic.net/geo/#1A0.0A1.3A0.3L2.3L6.6L4.4L8.6L5.5L9.5L7.7L11.4L7.7L15.7A3.23L22.23L29.24L21.21L36.30L35.29L36
Pingback: pascal
Hi all,
Just a question to understand the rules: In the following example, following the paradigm that lines should have infinite length (extend for free), shouldn’t I be able to create a circle with its center at the intersection of the line and the circle on the OUTSIDE areas (left or right)?
http://sciencevsmagic.net/geo/#0L1.0A1.1A0
On paper that would work of course, but here I do not get an option to snap to that intersection.
You’ll have to first click on a point along the line you want to intersect and extend it out to the point you describe. The intersection at that point will otherwise remain hidden.
But as you say, extension is free.Because the line already exists this won’t count as a move for the purposes of the challenges.
Pingback: Ancient Greek Geometry | Superlevel
Pingback: Google
Hi, found your site due to a recommendation in a local (German) computer magazine (c’t).
Simply great!
(Even with – or maybe due to – the “rudimentary” surface, I personally prefer prompts instead of windows).
Suggestion of mine for a new “challenge”: a=1 or r=1 rsp. (“origin line” instead of “origin circle”).
Some of these are already solved thru the current things but some of them (e.g. octogon) require more steps than the “independent minimum”.
Once again: Congratulations!
H.-C.
I really like this new challenge idea! Solving the octagon this morning was lots of fun. Thanks HC.
If I make version 2.0, it will have to include this!
Is this what you had in mind, an octagon where one side is the initial unit segment?
http://www.sciencevsmagic.net/geo/#0A1.1A0.0L1.3L2.6A0.1L8.8L11.0L11.11L12.12A0.0L16.1L17.11L20.16L20.12L21.1L10.10L17.17L32.32L21.21L34.34L20.39L21 (15 moves)
Nicely done, my best was 15 as well.
http://sciencevsmagic.net/geo/#0A1.1A0.0L1.2L3.6A0.8A0.3L12.12A0.7L0.0L13.7L1.1L14.12A7.0L25.25L13.13L33.1L26.26L14.14L37.37L33.32L42.41L36
Aha—but one of your circles is unnecessary, so you can do it in 14 moves, matching the origin circle record.
This toy is so simple, so profound and so beautiful. Thank you! I have a copy of Euclid’s Geometry and would like to work through it using your program as an aid. Is there any chance you might add the option of disabling the challenges and the search algorithm that goes along with them? I guess what I’m asking for is… creative mode! Seriously, thank you so much for this truly wondrous little thing.
Thanks Aaron.
If the challenges box is bothering you, the best solution might be to hide the div using a browser extension. The search algorithm won’t do too much then apart from the occasional shading (which becomes less often as your solutions fill in).
The challenges never change what you have drawn, so I see the default as “creative mode”.
great app! Holy that 8-move square was hard. Anyway, this should be a challenge as well:
http://sciencevsmagic.net/geo/#0L1.0A1.1A0.1A2.0L2.1L5.5L6.5A0.6A5.5A1.11A6.2A0.2L27.27A2.27L30.30A27.11L22.6L11.30L33.33A30.33L36.19L21.N.33A30.34L31.31L28.28L23.23L4.4L15.15L16.16L21.19A16.18A17.35L32.32L29.29L74.74L73.74L17.36L33.17L20
😀 (be warned its a little crude)
What the smallest number in challenges mean? Is it just for simple case or for the “origin circle” case too?
PS. Question is because the best I have for “circle pack 7 in origin circle” is 15, not 14. 🙂
Yes! Now I have 14! What a fun! 🙂
I have overlooked a simpler challenges again and it looks like that small number is not always achivable with “origin circle”. It is obvious for some cases. So I was overtrying with “circle pack 7”. 🙂
For some additional fun:
* Draw an equilateral (triangle, square, pentagon, hexagon, etc.) that is exactly tangent to the origin circle (my current best: triangle, 9 moves; square, 12 moves; and hexagon, 15 moves)
* Construct a set of Pythagorean 3-4-5 squares (my current best is 27 moves, but it’s probably possible to do much better than that)
* Duplicate the effort of Dürer & Pacioli, et al., and use the compass & straightedge technique to construct “perfect”-weight Roman-style serif letters (e.g. http://www.identifont.com/show?DGK or http://luc.devroye.org/fonts-41587.html), though that might be too hard without a “marked ruler” or a “fixed compass”
origin circle circumscribed triangle: 6 moves
origin circle circumscribed square: 10 moves
origin circle circumscribed hexagon: 11 moves
It would be helpful if I could delete or hide lines and circles.
It would be much easier if I could delete things that I know are only for previous constructions.
By the way, this game is great! I just wanted to say that it is a really fun and challenging game.
Can someone explain the circle four pack in 12 moves? It’s driving me crazy.
Hi, it’s H.-C. again.
I had a break and today (boring Sunday) remebered this tiny little fun.
In case of “Version 2” (or whatever number) what about an option to fill regions with “black” (I think colors would not be convenient for this page). Something like “right click” etc.
So to have an opportunity to create “something”, then press E to have all lines in gray, fill all necessary areas and see what you tried to create …
My first idea was according to the Euro symbol – unfortunately this needs an nonagon which is impossible to be created. Nevertheless it would be a great fun to do something like this …
hi all 🙂 i was trying to see if this functioned in your thingy:
http://omnicentre.ca/ultima/Visualizations/trianglesandSquares.swf
and i got to about here (which has the pentagon facing the opposite direction, at this point i’d need to make another 5 of the pentagonal guides in the other plane but the graph is just too complex at this point to pin properly)
which is sorta pretty in its own right 🙂
http://sciencevsmagic.net/geo/#0A1.1A0.2A0.4A0.6A0.8A0.3A0.6L2.2L3.3L6.N.4L3.6L1.2L8.N.0A25.0L7.0L29.0L12.0L30.52A0.56A0.68A0.51A0.87A0.55A0.N.55L56.56L51.51L55.47L4.47L8.28L2.28L3.53L87.53L68.N.54L53.54L145.154A53.206L54.54A206.54L255.54L256.255A54.255L360.377A255.360L441.441A366.441L256.256A54.N.255L54.256L54.441L256.441L360.360L255.55L56.55L51.51L56
can anyone tell me if that flash file i pointed to is actually geometrically true? I’ve done a lot of versions by hand and it seems really, really close, but without the whatnots to pin it too I can’t really tell if this is actually the construction to make the perfect square-inside-the-triangle or not. <3
This is brilliant. I am having a fun time with it, and it’s 90 degrees F outside in PR.
“What is Mathematics” by Courant and Robbins has a brief but concise description of constructions, up to finding a square root.
Maybe version 2 could have one free point as well, that the user could position at the start. Check out my geometry program GEOSTRUCT on mathcomesalive.com
Very nice application! The challenges are very fun and at some points.. frustrating. 🙂 Overcoming the frustration and completing the puzzles has been gratifying.
A suggestion: to rotate the view/change the viewing angle. New perspectives open new posibilities.
Is there a way to trisect or pentasect an angle?
It doesn’t seem to recognize my pentagon.
http://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A2.2A1.5L0.0L4.1A0.9L10.14A7.7A24.27L7.7L28.28L10.8A10.10L70.70L27
Based on http://www.cut-the-knot.org/pythagoras/pentagon.shtml
Hi, is there a way to reset certain completed challenges?
http://www.sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A1.0A5.5A0.14L15.18L5.5L20.18A20.18L21.21A33.18L0.0L44.44A45.18A19.N.18A20.5A1.18A19
If the biggest circle has a radius of one unit, how large are the radii of the smaller two?
In case anyone cares, I found out that if x idthe smallest circles radius, then x(sqrt(2)+1) is the next circles radius and x(sqrt(2)+1) + x is the largest circles radius
Finally! I got the circle pack 7 in origin circle. I fiddled with it a while and tried to shrink my pack 7 into the origin circle.
Mascheroni had a compass only five step construction that gives the golden section. An additional two steps lays out the five points of a pentagon which gives us a 12 step construction. See: http://www.cut-the-knot.org/pythagoras/MascheroniPentagon.shtml for more info. Here is the solution: http://www.sciencevsmagic.net/geo/#0A1.1A0.3A2.0A5.1A4.8A3.9A3.2L13.2L12.12L21.21L20.20L13
That someone found a way to do it in eleven is amazing, might be worth publishing it.
I managed to get it down to eleven by extending the first two sides, and using the larger circle. A new record for me!
I wonder if this is the same as Anders’ solution.
Thanks for the suggestion. It worked. This program strikes me as really hitting a sweet spot in the realm of puzzles. Do you mind if I hack away at your code? I would like to make a much simpler version. I’m hoping to interest my 8 year old daughter with it.
A student of mine found a 9 steps construction for the 3 circle packed in the original circle. I googled a lot but i did not find anything about. Is this interesting?
I apologize for the mistake. The 3 circle packed in the original circle construction has 10 steps…
Is it possible to modify the original post (9 steps -> 10 steps) and delete this couple of replies, pls?
What a nice blog site it is ! It is a historical and informational site of geometry It discus with science vs magic I have visit this site and play this game and enjoy interesting.Recently I have seen a site like this It is ancient geometry for more information just click here,thanks.
Hi. Sorry to bother you but how “in origin circle” is different than “constructed”? I’ve made such a hexagon without the circle that contains the hexagon being the first one made:
What did I do wrong? Hexagon can’t touch the same circle with every corner?
Sorry, I’m not quite sure what you are asking.
The constructed challenge is awarded the first time you construct the shape, which may or may not be at the same time as other challenges.
It’s possible to have one solution qualify for multiple (or in some cases even all) challenges for a given shape.
Now I understand, thanks.
My mate just managed the 2-GON in 15 moves!
http://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A0.3L1.1A0.1L10.1L8.8A10.14A6.3A6.10L4.6L29.29L38.38L37.37L15.15L4.4L3.3L6
I’ve made 16-gon, 32-gon and 64-gon. Quite boring but I’d like to have all existing challenges. Are there infinitely many challenges (for 2^k-gons)? If not – what is the limit for k? If so – why are you so cruel? 😛
Now I see that there are infinitely many hidden challenges for every k-gon (where k e N and k > 1).
By the way, I managed to construct an inconstructible polygon – heptagon with error 0.0003, building on this algorithm:
http://www.geocities.ws/london_blue_catharin
And here is is:
If you consider it a bug and want to get rid of it here are n’s for which n-gon is inconstructible:
https://oeis.org/A004169
…and I’ve written a program in JavaScript that given x prints all inconstructible polygons with less than x edges:
http://ideone.com/EAGOTh
It’s based on the necessary and sufficient condition for polygon to be constructible:
“A regular n-gon can be constructed with compass and straightedge if n is the product of a power of 2 and any number of distinct Fermat primes.”
The program is simplified and works “only” for polygons with n <= 2^32. Quite practical though.
Woot!!! Same algorithm, 43 moves…
Wow! I beat myself in 10 minutes lol…
Whoa… got the 9-gon done too (the one with 0.0002° error)
Just a HINT. If you want to look at somebody’s solution and not have it remembered as yours in your cookies, open the link in Incognito aka Private mode. In Chrome Ctrl+Shift+N and in Firefox Ctrl+Shift+P.
So I was puzzling over the dodecahedron (and other puzzlements), and was staring at your homepage, and realized I was staring at the solution (I think). Don’t know if you care, but perhaps you might want to switch the design that links to the game/application to something that isn’t a solution to one of the later puzzles?
I finally found a way to dodecagon in 20 moves
http://sciencevsmagic.net/geo/#0A1.1A0.2A0.2L3.2L6.4A0.5A1.0L7.7L1.9L6.6L11.6A2.9L26.26L4.11L27.27L5.7A2.1L55.55L5.0L56.56L4
now the game is beaten!!
Hi,
Can anyone explain me why the game does not accept my pentagon (12 moves, not in origin circle) ?
http://www.sciencevsmagic.net/geo/#0A1.1A0.2L3.3A0.6L5.6L4.6L12.6L8.8L0.0L1.1L12.12A1.2L32.32L12.32L8
Dodecagon in 19 moves:
http://sciencevsmagic.net/geo/#0A1.1A0.2L3.0L1.0L5.2L5.5L3.5A0.8L7.7L1.1L8.N.0L22.22L26.0L25.26A0.25A0.27L25.41L26.40L26.28L25.27L28.41L40
Hi,
I can’t help but wonder if the challenge to complete the in-origin-circle triangle in 5 moves is a mistake. The way I see it, you use 1 move to create the circle, then you will use 3 to create the triangle, so you have just 1 other move to set up the triangle. After creating the origin circle, there are only 2 other possible moves, neither of which set up the triangle. Am I missing something, or is the right column supposed to read 6 for the triangle?
Thanks!
5 steps is correct.
Hint: the triangle is equilateral and you can set up the three vertices in just two moves.
Thanks for the reply. Certainly a triangle is easily constructed in 5 moves, but I’m talking about the triangle specifically inscribed in the origin circle. First move is drawing the origin circle. The only other possible moves after that are to draw a congruent circle centered on the other non-origin point, or draw a radius or diameter line on the origin circle. Neither of those second moves sets up the three vertices of a triangle inscribed in the origin circle.
The origin circle challenges are different from the minimal move count challenges. There’s one prize for getting it in 5 moves any old way, and another prize for getting unit circle in any old number of moves.
why doesn’t it work
http://sciencevsmagic.net/geo/#0A1.1L0.1A0.3L4.6A0.0L2.2A0.10L9.12A0.3A6.10A12.37L0.0L40.14L8.41A0.13L7.50A0.0L13.13L68.7L0.0L74.0L67.41L12.39A0.40A0.47L106.2L40.130L115.115L129.134L157.150L165.165L189.150L186.42L119.124L9.129L283.318L189.47L48.44L49.49L48.47L408.44L408.448L479.47L495.495L44.536L568.47L583.44L583.626L657.626L568.657L704.704L762.762L536.704A40.62L61.53L62.56L61.53L831.831L56.1019L976.56L1036.53L1036.1152L1106.53L1169.56L1169.1290L1242.1152L1290.1106L1242.1355A39.N.68L0.0L73.0L67.0L74.704A40.1355A39.68L74.1355L1497.704L1497.1119L326.1119L130.1642L326.326L1779.1779L1882.1779A2.91L102.98L102.102L2017.104L91.98L1951.104L1951.2177L2242.98L2254.104L2254.2361L2424.104L2436.98L2436.2613L2549.2361L2549.2424L2613.2687A1.0A1
circle pack 4 in origin circle is all i have left and i don’t know why it works help!!!!
feel free to take my other solutions
still need help
the circles arent touching the line
First time I made a pentagon it was in thirteen moves like so…
http://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A0.1A2.6L3.0A9.9L12.9L13.12A9.12L32.13A9.13L50.50L32
after further work I found a way to make a 12 move pentagon… http://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A0.1A2.4L7.0A9.12L9.9L18.9A18.9L13.12L27.27L26.26L13
all hail my brilliance! This
I used your technique and reduced it to 11 moves http://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A0.1A2.4L7.0A9.12L9.9L18.18L13.13L27.9L13.9L30.30L12.12L38.38L27
But I don’t understand what you did in the first place! Hail!
I’ve found you can get the origin circle achievement in 11 too, but it’s a bit of a cheat…
http://www.sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A0.6L3.1A9.12L9.9L16.13L9.9L21.0L4.4L12.16L21.13L4
It’s not accurate enough. 17-gon construction resulted in a 22.2-gon
If you’re following the recent Numberphile post, be aware that the paper version contains an error (which they get right in the computer graphics).
I followed the correct version and managed a 17 gon after a few attempts:
http://www.sciencevsmagic.net/geo/#0A1.1L0.0L2.2A1.1A2.4L5.2L3.3A2.10L9.3A12.3L11.15A12.11A3.22L21.15A3.11L33.33L36.3L36.36A43.36L56.1L43.1L56.57A73.73A86.86A73.102L101.122A73.73A122.138L137.137L143.73A85.85A73.190L189.73A214.214A73.246L245.245L251.0A143.N.251A1.1A251.331L332.347A1.279A382.412A279.413A279.N.279A434.434A279.462A279.575L576.533L532.576L592.532L617.N.0A1.592A617.643A592.677A643.591A677.616A591.786A616.839A786.882A839.617A592.949A617.986A906.1024A986.1068A1024.1121A2.2A1121.1232A2.916A882.916L592.592L1232.1232L643.643L2.2L677.677L1121.1121L591.591L1068.1068L616.616L1024.1024L786.786L986.986L839.839L949.949L882.882L617.617L916
The junk out to the left is a way of doing the early bisections without cluttering up the circle so much.
Whew. Just bruteforced my way through a 42-step 7-pack in-origin. Not sure what an “ideal” solution would be, but I’ll be damned if I didn’t make mine work.
Word to the wise, don’t…
Nonagon 9 – gon (from wikipedia)
SPOILER:
http://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A2.2A1.5L4.7A0.9L10.10L18.9L19.N.1A0.7A0.25L1.N.7A16.25A29.25L30.N.37L47.47L49.N.25L0.N.1A56.56L64.N.19L18.37L49.64L81.0L79.79L92.1L92.0L106.1A121.130L121.121A130.121L21.21A121.21L211.211A21.211L262.130A121.130L22.22A130.22L331.331A22.331L363.363L2.2L262
and aproximated heptagon
SPOILER:
http://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.2A0.7L1.3L0.1A11.12L0.N.0L12.1L12.12A1.13A1.26A12.40A13.N.1L12.12L26.26L49.49L61.61L40.40L13.13L1.61L12.12L40.61L1.1L49.49L13.13L26.26L40.0A1
Heptagon!
Spoiler:
http://sciencevsmagic.net/geo/#0A1.1A0.1L0.2L3.6A0.1A6.1L5.0L4.13A1.6A4.4A6.N.2L3.0L1.5A6.N.6A0.5A6.0L31.31L41.31A0.5L39.39L61.N.6A13.13A6.1L91.91L104.0A6.76A0.121L120.123A4.6A20.4A123.123A29.183L98.98L202.N.5A202.217L5.5L218.218A5.217A5.217L293.218L265.265A218.293A217.391A293.293L391.391L349.349L265
17- gon (from gaussianos.com)
http://sciencevsmagic.net/geo/#0A1.0L1.0L2.1A2.2A1.5L4.7A0.9L10.N.0L16.0A16.16A0.26L27.N.1L30.30L8.30A7.25A58.58A25.91L30.N.30L8.30L103.30A7.115A25.25A115.137L30.N.30L137.30L155.30A75.168A169.169A168.30L200.200L225.30L199.199L222.N.30L160.30L222.168A232.232A168.30L265.0A1.9L10.26L27.222L228.265L292.30L211.30L225.N.278A1.278L1.1A278.359L360.376A1.N.0A1.376A1.142L425.142A425.495A506.514A513.513A514.544L495.495L558.494A92.597A92.92A597.634L633.633L646.558L0.646L0.N.0A1.646A558.558A646.839L0.N.0A1.869L558.646L869.646A869.957A646.755A957.1002A755.1023A1002.1046A1023.1057A1046.645A1057.1085A645.557A1085.1122A557.1148A1.1A808.808A1.1209A558.1002L1023.1002L755.755L957.957L646.1023L1046.1046L1057.1057L645.645L1085.1085L557.557L1122.1122L1148.1148L1.1L808.808L1209.1209L558
I haven’t played this in way too long what an amazingly simple but fun game i’m gonna do all the challenges again and continue work on way to high number gons
Why doesn’t this :
http://sciencevsmagic.net/geo/#1A0.0L1.1L2.0A2.2A0.4L1.1L5.7A4.8A5.0L8.0A22.2L7.2A34.1A28
register as the solution to Circle Pack 4 (in origin circle) ?
The circles at top and bottom are popping out of the circle.
The ancient Greeks performed geometric constructions with only a simple compass and straightedge, and a Persian mathematician Abul Wefa proposed the “rusty compass” (fixed radius compass) principle. This set of drawings illustrates it: http://www.glennwestmore.com.au/geometric-constructions/
I believe https://sciencevsmagic.net/geo/#1A0.0A1.0L1.1L4.4A1.6L7.3L2.4A9.0A10.0A9.4A10.28L1.1L29.2L34.34L7.7L12.12L4.4L11.11L6.6L33.33L3.3L15.15L0.0L14.14L2 is a regular dodecagon in 23 steps but it’s not being recognized. Totally stymied on getting to 20 steps!
It’s close, but this isn’t a regular dodecagon. That a look at https://sciencevsmagic.net/geo/#1A0.0A1.0L1.1L4.4A1.6L7.3L2.4A9.0A10.0A9.4A10.28L1.1L29.2L34.34L7.7L12.12L4.4L11.11L6.6L33.33L3.3L15.15L0.0L14.14L2.2A34 this new circle shows that two sides aren’t even.
I made a 48-gon!
https://sciencevsmagic.net/geo/#1A0.0A1.2A0.4A1.6A1.8A1.3A0.12L7.11L9.5L10.13L3.3L15.15L0.0L17.17L2.2L14.14L4.4L16.16L6.6L18.18L8.8L13.1L6.1L91.6L92.17A0.0A15.15A0.3A13.13A3.8A13.18A6.6A16.16A4.4A14.14A2.2A14.180L179.173L172.164L165.156L155.145L146.139L138.129L130.122L123.115L114.104L105.96L94.95L93.215L17.17L211.211L0.0L207.N.215L17.17L211.211L0.0L207.207L15.215L2.2L195.195L14.14L200.200L4.4L204.204L16.16L208.208L6.6L212.212L18.18L216.216L8.8L196.196L13.13L199.199L3.3L203.203L15.6A208.212A6.18A212.216A8.8A78.196A8.13A196.199A3.3A90.203A3.15A203.207A0.0A30.211A0.215A2.17A211.2A41.195A2.14A195.200A4.4A55.204A4.16A204.208A6.1322L1311.1306L1291.1270L72.1254L55.1259L1246.1240L1225.1204L60.1171L41.1192L1176.1191L1160.1138L48.1121L30.1126L1113.1108L1093.1072L34.1056L90.1061L1046.1042L1027.1006L23.990L78.995L982.977L961.937L83.938L66.N.1600L0.1578L0.211L1578.1552L211.17L1552.1528L17.215L1528.1508L215.2L1508.1486L2.195L1486.1460L195.14L1460.1436L14.200L1436.4L1416.1416L200.204L1394.1394L4.1368L204.16L1368.1344L16.208L1344.1599L208.6L1599.1577L6.212L1577.1551L212.18L1551.1527L18.216L1527.1507L216.8L1507.8L1485.1485L196.196L1459.1459L13.13L1435.1435L199.199L1415.1415L3.3L1393.203L1393.203L1367.1367L15.15L1343.1343L207.207L1600
I put up a gist of links with the best solutions I could find or invent:
[SPOILER]
https://gist.github.com/mrflip/a973b1c60f4a38fc3277ddd57ce65b28
[/SPOILER]
I still don’t have the circle pack 4.
Please fork the gist and add any improved solutions to it.
Not super efficient, but here’s a 19-pack: https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A1.0A5.0L2.2L14.0L13.0L11.0L3.3L17.0L16.14A2.16A15.11A4.13A12.17A3.0A8.16L4.16L39.27A8.39L46.0L26.26L56.2A0.57L0.57L63.63L65.16L23.23A54.63A23.82L83.83L0.90A35.82L114.N.0A114.90A35.16A15.14A2.5A1.0A1.17A3.13A12.11A4.17L14.14L146.0A90.166A113.17L145.4L125.161A38.132A130.11L118.5L119.0L121.166L0.166L207.121A207.215L0.237A215.0L6.6L260.260A119.119A260.292L0.316A263.0L17.0L120.17L123.0L259.0L236.0L315.238A236.317A315.237L16.16L361.362L0.362L383.362A339.0L384.385A325.385L5.5L420.421L0.0L443.421L442.421A412.444A443.N.0A1.13A12.238A180.317A315.362A339.11A4.16A15.421A412.90A35.166A113.237A215.316A263.385A325.444A404.132A130.N.161A38.17A3.13A12.132A130.444A404.385A325.5A1.316A263.237A215.166A113.90A35.421A412.362A339.317A315.238A180.11A4.16A15.14A2.0A1.0A114
And here is a 6-move origin circle circumscribed triangle: https://sciencevsmagic.net/geo/#0A1.1A0.3A2.4L2.4L3.3L6.6L5.5L7.7L2
Here is the in-origin 4-pack in 13 moves: https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.0L4.2L3.6A0.0L7.7L10.0L9.10A5.0A15.15A4.24L0.0L35.24A35.25A1.0L36.38A36
I have no idea how 12 moves is possible…
I finally figured out an in-origin 4-pack in 12 moves!!
https://sciencevsmagic.net/geo/#0A1.1A0.2A3.2L1.1L6.6L0.9A11.0A18.18A9.0L21.21A10.2L0.0L34.33A2.34A30
Hi John,
That’s amazing. It would be much appreciated the math behind it. I don’t get why it worked!!!
Here is an actual pentagon (not just the star) in the origin circle in 11 moves: https://sciencevsmagic.net/geo/#0L1.0A1.0L2.1A2.2A0.5L6.1A9.1L3.16L13.16L12.23L19.13L2.2L12
Here is an in-origin circle pack 3 in 10 moves: https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.0L4.5A2.6A0.0A10.10A1.15A0.26A18.25A19
Not super efficient or in origin circle, but here’s a circle pack 5: https://sciencevsmagic.net/geo/#0L1.0A1.0L2.1A2.2A0.5L6.1A9.1L3.16L13.16L12.23L19.13L2.2L12.12L0.0L46.23L0.0L53.13L0.0L60.19L0.0L68.N.2A1.75L74.105L23.108A26.N.0A108.N.137A60.139A67.135A52.133A45.0A26
Can’t figure out the 23 move version, but here’s a 16-gon in 24 moves: https://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A1.1A2.4L5.1A7.1L11.11A7.11L17.N.0A1.17L7.17L8.7L21.8L27.0A17.27L35.21L34.8L33.33L32.2L31.31L8.8L43.43L19.19L56.31L7.7L65.65L25.25L78.34L66.66L89.35L58.58L99.78L92.92L113.111L108.108L2.2L125.125L32.32L1.1L143.101L47.47L149.149L89.143L82.82L165.33L169.169L178.125L69.69L190.190L99.178L160.165L56.101L160.113L33
31-pack: https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.0L4.2L0.0L6.0L3.0L7.5L7.0A8.8A2.0A22.14A1.17A3.15A6.13A4.16A7.16L8.8L49.49L46.13L15.15L54.54L46.54A52.0A54.4L67.75A51.17L15.15L93.93L92.92A90.93A91.6L70.15L76.76A57.13L16.16L116.116A115.54L116.4A13.67L137.137A4.0A137.7L161.161A7.2L159.159A2.70L160.160A6.3L162.162A3.158A1.13L133.137L140.13L17.17L213.213L54.0A213.213A61.213L137.137L253.253A252.236A84.236L31.31L240.240A117.240L241.241A123.241L8.8L237.237A110.0A259.253L27.27L363.363A321.240L160.160L244.244A313.14L16.16L53.53A62.14L238.238A98.53L161.161L446.446A259.238L239.239A104.0L53.53L529.0A526.N.0A526.237A110.253A565.446A259.236A84.238A98.244A313.160A6.93A91.137A4.54A52.161A7.116A115.159A2.75A51.158A1.92A90.17A3.15A6.13A4.16A7.8A2.0A22.14A1.363A321.241A123.53A62.213A61.239A104.240A117.76A57.162A3
37-pack:
https://sciencevsmagic.net/geo/#1A0.0A1.1L0.0L5.3L1.3A0.0L7.1A10.1L19.19A3.22L21.5A0.8L34.1A5.5A1.60L9.5A69.70A1.97L96.0A18.0A97.140L160.162L29.29L192.192A1.213A8.8A213.1A192.277A1.302A34.34A302.341L34.34L302.302L277.277L1.1L192.192L213.213L8.256L8.256L341.N.34L0.0L3.341L0.0L585.256L0.0L618.1L5.277L0.0L634.8L0.0L2.302L0.0L678.192L0.0L701.281L204.213L0.0L773.634L5.5L701.701L773.773L2.2L610.610L585.585L3.678L3.678L634.N.0A367.828A537.798A537.797A632.1065A632.1064A676.500A676.1030A564.995A564.448A583.960A583.959A608.928A608.927A653.894A653.386A770.861A770.860A699.367A699.0L894.1437A894.1453A1437.0A1453.959L0.1571A1570.995L0.1629A1626.0L1064.1534A1436.0L798.1572A1567.0L860.1630A1627.1453L860.1719A1756.0A1716.1453L928.448L894.1843A1934.0A1756.1840A2023.1850A2025.629A2027.1839A2029.1630L1534.828L0.0A2232.367L1839.1839L2347.2232L2387.2232A2448.2387A2448.0A2448.2387L2588.2588L2711.2711A2588.2711L2612.2612L2325.2325A2612.2325L2606.2606L2975.2975A2606.2975L2611.2611L3092.3092A2611.0A2546.798L1568.0A1214
Kind of silly but due to the floating point, an 18-gon: https://sciencevsmagic.net/geo/#1A0.0A1.1L0.0L5.3L1.3A0.0L7.1A10.1L19.19A3.22L21.5A0.8L34.1A5.5A1.60L9.5A69.70A1.97L96.0A18.0A97.140L160.162L29.29L192.192A1.213A8.8A213.1A192.277A1.302A34.34A302.341L34.34L302.302L277.277L1.1L192.192L213.213L8.256L8.256L341.N.34L0.0L3.341L0.0L585.256L0.0L618.1L5.277L0.0L634.8L0.0L2.302L0.0L678.192L0.0L701.281L204.213L0.0L773.634L5.5L701.701L773.773L2.2L610.610L585.585L3.678L3.678L634
Some squares are recognized. Others aren’t. Why?
https://sciencevsmagic.net/geo/#1A0.0A1.3A0.4A1.6A1.7A3.0L10.10L11.11L6.6L0
It’s not square; the circle I added on the top right corner would meet its two neighbors if the rectangle had equal sides
https://sciencevsmagic.net/geo/#1A0.0A1.3A0.4A1.6A1.7A3.0L10.10L11.11L6.6L0.N.11A3
heptadecagon ( 17-gon ) in 59 moves according to https://commons.wikimedia.org/wiki/File:01-Siebzehneck-Variation.svg :
https://sciencevsmagic.net/geo/#0A1.1A0.0L1.0L4.4A1.1A4.10L9.2L3.0A14.14A0.24L25.25L30.24L29.28L12.28A0.0A52.52A0.28L71.93A0.0A93.N.108L28.78A28.12A151.151A12.186L187.200A12.115A232.N.258A256.287A286.286A287.N.340L339.0A1.361A12.362A12.385A212.426A211.461A385.507A426.558A461.610A507.656A558.710A610.762A656.821A710.879A762.947A821.12L821.821L656.656L362.362L947.947L558.558L426.426L1071.1071L461.461L507.507L1010.1010L385.385L610.610L879.879L361.361L710.710L762.762L12
hendecagon (11-gon) according to https://commons.wikimedia.org/wiki/File:01-Elfeck-3.svg :
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.3A0.0L3.3L9.9A3.9L11.11A9.11L14.14L4.15A1.24A15.30L29.24A33.15A33.1A52.0A61.61A1.76L77.1L81.0A81.0L10.0L113.33A15.122A33.131L130.130L137.114A137.114L168.2A68.193A2.198A193.203A198.2A208.1A15.112A114.240A112.244A240.247A244.249L248.247A255.250A272.112A275.81L5.80A1.300A80.307A300.312A5.317L318.323A307.323A33.312A323.377A5.383L382.81A387.2L217.0A137.440A0.103A445.68A0.61A0.N.114L158.61A52.61L541.2L215.61A15.61L616.112A255.112L670.33A323.33L730.61A387.61L829.2A445.2L896.61L99.68L468.61L482.482L468.468L1085.1085L99.99L1127.1127L896.896L1205.896L1197.894L829.829L1239.1239L730.730L1290.1290L670.670L1337.1337L616.616L93.93L215.215L1514.213L541.541L1554.1554L167.N.2A1608.1647A2.1608A2.1707A1608.1670A1647.1797A1670.1751A1707.1864A1751.0A1.1826A1797.1972L1912.1912L1864.1864L1751.1751L1707.1707L1608.1608L2.2L1647.1647L1670.1670L1797.1797L1826.1826L1972
you guys are masters I can’t even do a pentagon
I’m working on a list of polygons. Here is the partial list, if anyone has a 25-gon, I really need it.
Some are my work. Otherwise, I found it in the comments on github. (Ctrl + f, github)
2-gon
https://sciencevsmagic.net/geo/#0L1.1A0.1L2.2A0.2L3.3A0.3L4.4A0.4L5.0A5.0L6.0A1.12A0.12L11.33L6.33L38.5L33
3-gon
https://sciencevsmagic.net/geo/#1A0.0A1.1L0.1L3.0L3
4-gon
https://sciencevsmagic.net/geo/#0A1.1A0.2A3.2L0.0L6.2L7.N.7L4.9L1.8L4.8L15.1L15
5-gon
https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A0.5L8.N.2L7.5A9.N.15L16.14L16.23L19.14L0.0L15
6-gon
https://sciencevsmagic.net/geo/#1A0.0A1.3L0.0L4.N.1A4.4L6.4L2.2L8.8L6.5L10.10L11.11L7.7L12.5L0.0L2
7-gon(Made from 14-gon)
https://sciencevsmagic.net/geo/#1A0.1L0.0L2.2A0.0A2.1L5.0L6.6A0.2A1.6L11.11A16.5L21.2L3.16A11.3L24.24A21.1A34.34A1.55L54.0A58.58A0.91L92.0L99.99L58.0A99.152L0.59L152.59A152.58A99.58L221.59L207.221L80.80A221.80L298.298A80.298L330.207A59.363A207.207L363.363L376.376A363.376L100.100L2.2L330.N.298L2.2L376.376L207.207L152.152L99.99L221.221L298
8-gon
https://sciencevsmagic.net/geo/#1A0.0A1.3A0.5L1.1L7.4A6.1L11.1L12.11L13.N.7L12.12L4.6L13.13L2.12L16.16L6.33L4.6L30.13L30.30L2.2L46.46L7
9-gon
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A2.2A1.5L4.7A0.9L10.10L18.9L19.N.1A0.7A0.25L1.N.7A16.25A29.25L30.N.37L47.47L49.N.25L0.N.1A56.56L64.N.19L18.37L49.64L81.0L79.79L92.1L92.0L106.1A121.130L121.121A130.121L21.21A121.21L211.211A21.211L262.130A121.130L22.22A130.22L331.331A22.331L363.363L2.2L262
10-gon
https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A0.6L3.0L4.N.1A9.12L1.1L13.14L13.13L30.14L12.12L37.0A14.13L48.12L47.37L50.30L49.4L49.48L54.30L59.50L4.47L70.76L37
11-gon
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.3A0.0L3.3L9.9A3.9L11.11A9.11L14.14L4.15A1.1A15.31L32.1A35.0A54.54A1.71L72.0A75.N.0A24.2A112.0L10.126A0.137L138.1L54.54A35.117L174.174L192.192L162.N.0A1.205A2.218A205.2A205.250A2.234A218.267A250.282A234.302A267.344A302.2L205.2L250.250L267.267L302.302L344.344L360.360L316.316L282.282L234.234L218.218L205
12-gon
https://sciencevsmagic.net/geo/#1A0.0A1.3L0.0L4.4L1.1L6.2L5.5L8.N.1A8.0L5.5L18.0L17.8L3.3L22.2L14.22L14.6L26.26L32.6L31.18L27.27L37.37L21.21L17.32L2.2L9.9L31.54L0.54L63.63L36.36L70.70L41
13-gon
https://sciencevsmagic.net/geo/#1L0.0A1.1A0.0L2.2A0.2L8.8A2.8L11.11A8.11L14.14A11.14L17.17A14.17L20.20A17.20L23.23A20.25L24.1L5.5A0.0A14.30A0.5L30.35L36.5A1.40L41.5A45.38A43.59A38.66L67.44A5.56L79.39A44.114L113.56A39.79L138.138L5.5A138.172A27.27A172.203L202.219A27.35L242.59A43.43A44.38L296.39A72.296L359.359A0.359L394.394A366.366A394.453L454.66L476.43A5.496L495.495L511.511A476.595L56.599L242.N.242L5.599A503.727A599.749L599.749A599.825L727.0A714.727L956.956A955.955A956.1043L1042.1043L0.0A1.1077A1.1119A1077.1144A1119.1168A1144.1186A1168.1202A1186.1A1077.1226A1.1253A1226.1275A1253.1299A1275.1317L1214.1214L1202.1202L1186.1186L1168.1168L1144.1144L1119.1119L1077.1077L1.1L1226.1226L1253.1253L1275.1275L1299.1299L1317
14-gon
https://sciencevsmagic.net/geo/#1A0.1L0.0L2.2A0.0A2.1L5.0L6.6A0.2A1.6L11.11A16.5L21.2L3.16A11.3L24.24A21.1A34.34A1.55L54.0A58.58A0.91L92.0L99.99L58.0A99.152L0.59L152.59A152.58A99.58L221.59L207.221L80.80A221.80L298.298A80.298L330.207A59.363A207.207L363.363L376.376A363.376L100.100L2.2L330
15-gon
https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.0L4.5A0.6L3.1A9.N.2L12.12L18.3L13.13L22.18L3.3L27.22L2.2L31.22L26.26L18.0A26.3L41.41L4.4L49.49L50.50L12.12L56.2L39.39L4.4L68.68L69.69L13.13L75.56L75.27L43.43L49.49L106.31L44.44L68.68L114.56L96.96L106.75L81.81L106.126L31.56L62.114L62.154L27.106L129.114L143.126L143.31L42.42L22.18L40.154L129.27L40.114L97.97L75
16-gon
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A1.1A2.4L5.1A7.1L11.11A7.11L17.N.0A1.17L7.17L8.7L21.8L27.0A17.27L35.21L34.8L33.33L32.2L31.31L8.8L43.43L19.19L56.31L7.7L65.65L25.25L78.34L66.66L89.35L58.58L99.78L92.92L113.111L108.108L2.2L125.125L32.32L1.1L143.101L47.47L149.149L89.143L82.82L165.33L169.169L178.125L69.69L190.190L99.178L160.165L56.101L160.113L33
17-gon
https://sciencevsmagic.net/geo/#0L1.1A0.1L2.2A0.0A3.3A4.4A3.7L0.0L10.1L10.12A0.0A12.1L29.0A38.38A0.N.1L60.1L36.3L4.36A1.91A10.10A91.122L121.132A10.65A155.176A6.6A195.195A6.228L227.N.0A3.246A10.245A267.N.267L302.267L333.0A333.302L375.375L10.10L381.381L399.302L175.175L406.406L333.406L448.448L10.10L474.474L267.267L484.484L496.496L406.406L526.509L245.245L556.509L555.555L484.526L456.456L595.556L595.595L246.246L646.646L570.570L659.659L670.670L245.245L702.10L615.381L685.381L735.484L581.685L736.736L659.754L433.735L302.246L811
18-gon
https://sciencevsmagic.net/geo/#1A0.0A1.1L0.0L5.3L1.3A0.0L7.1A10.1L19.19A3.22L21.5A0.8L34.1A5.5A1.60L9.5A69.70A1.97L96.0A18.0A97.140L160.162L29.29L192.192A1.213A8.8A213.1A192.277A1.302A34.34A302.341L34.34L302.302L277.277L1.1L192.192L213.213L8.256L8.256L341.N.34L0.0L3.341L0.0L585.256L0.0L618.1L5.277L0.0L634.8L0.0L2.302L0.0L678.192L0.0L701.281L204.213L0.0L773.634L5.5L701.701L773.773L2.2L610.610L585.585L3.678L3.678L634
19-gon
https://sciencevsmagic.net/geo/#1A0.0L1.1L2.2A1.2L5.5A2.5L8.8A5.8L11.11A8.11L14.14A11.14L17.17A14.17L20.20A17.21L22.15L16.0A1.0L28.27A0.1L27.27L32.32L0.33A0.32L41.38L27.41A33.38L52.41L51.51A33.33A34.41L67.41L68.79A41.85L84.95A78.24A25.21A17.17L21.21L139.139L20.139L144.0A144.20L151.151L117.151A117.117A151.235L234.8A255.277A255.255A277.283L8.283L293.25L290.290A25.0L393.393A25.25A393.N.290A25.393A25.25A393.388A393.462A25.556A462.388L598.556L508.508A388.598A556.393L720.676L462.676A508.25L817.817A676.393L901.598A388.598L976.976L901.720A393.720L1053.817L1053.556A508.556L1153.1153A556.1153L1201.1201L388.462A676.676A462.1299L462.676L1309.1299A462.1299L1414.1414L508.25A817.1309L1535.1535L25
20-gon
https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.5A0.6L3.0L4.N.1A9.13A1.19L20.20L26.N.1L25.25L13.25L33.13L42.25L37.37L12.49L1.37L52.1L63.49L62.12L53.58L13.13L75.47L71.71L16.58L74.47L86.5L8.67L12.12L97.79L97.97L110.67L100.79L104.0L104.92L16.16L125.104L125.125L140.140L131.92L117.117L110.110L154.154L146.0L146.4L131.131L154.146L140.140L183.154L171.172L169.172L194.160L182.199L196.185L212.243L4.4L26.227L26
21-gon
https://sciencevsmagic.net/geo/#1A0.1L0.0L2.2A0.0A2.1L5.0L6.6A0.2A1.6L11.11A16.5L21.2L3.16A11.3L24.24A21.1A34.34A1.55L54.58L0.0L59.58A0.100L58.100L118.118L59.1A118.100L150.58L157.157L59.59L179.150L179.12L13.100A12.12A42.13A41.179A13.267L179.179L13.13L258.250L12.12L100.100L237.250A12.250L162.162A250.162L484.258A13.201L258.201A258.201L571.571L484.237A100.237L656.656A237.656L58.58A656.58L760.760A58.760L815.815L0.0A815.267A179.267L936.936A267.936L59.59A936.59L1043.1043L916.916L0
22-gon
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.3A0.0L3.3L9.9A3.9L11.11A9.11L14.14L4.15A1.1A15.31L32.1A35.0A54.54A1.71L72.0A75.N.0A24.2A112.0L10.126A0.137L138.1L54.54A35.117L174.174L192.192L162.N.205A2.2A205.241L242.2A257.234A269.205A257.218A291.279A234.315L279.279L234.234L269.269L2.2L257.257L205.205L291.291L218.218L305.241L256.256L1.305A218.305L579.315A279.315L623.623A315.623L663.663A623.663L705.256A1.1A256.766L1.256L745.745A256.866L745.866L705.766A1.952L766.952A766.1019L952.1019A952.1019L1080.1080L579
23-gon (none)
24-gon
https://sciencevsmagic.net/geo/#1A0.0A1.3A0.2L3.3L7.7L1.N.8L3.1A0.3L11.11L2.1A11.2L24.8L23.23L24.1L22.14L28.28L33.33L8.8L42.42L15.15L32.14L32.16L3.3L57.57L27.27L66.66L2.2L16.48L37.37L86.86L31.31L96.96L45.45L85.85L48.105L0.0L18.18L4.4L135.135L95.95L122.148L9.9L164.122L105.164L0.0L17.17L4.4L163.163L9.184L180.54L215.180L221.221L9.73L262.9L263.184L220.220L198.198L263.65L302
25-gon (some attempts, but they didn’t work)
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.3A0.1L3.3L9.9L4.9L0.0A10.10A0.26L25.30A2.30A1.25L51.10L45.73A64.64A79.79A64.73L99.14A0.120L121.144A0.0A144.181L180.180L209.209A191.209L217.217A191.191A217.223L230.230L235.235L99.181L206.N.196L235.196A257.257A196.312L313.343A344.344A343.400L401.0A1.313L344.1L432.432A1.485L432.485A432.485L539.1A432.1L606.606A1.606L660.660A606.706L660.706A660.706L750.433A2.2L433.433L801.539A485.539L852.852A539.852L11.11A852.1002L11.2A433.2L1076.801A433.801L1120.1076A2.1160L1076.1160A1076.1209L1160.1209A1160.1209L1265.1265L1002.1120A801.1120L1376.1376A1120.1376L1425.1425A1376.1425L1479.1479L750
26-gon (tried to bisect 13-gon, didn’t work.)
https://sciencevsmagic.net/geo/#1L0.0A1.1A0.0L2.2A0.2L8.8A2.8L11.11A8.11L14.14A11.14L17.17A14.17L20.20A17.20L23.23A20.25L24.1L5.5A0.0A14.30A0.5L30.35L36.5A1.40L41.5A45.38A43.59A38.66L67.44A5.56L79.39A44.114L113.56A39.79L138.138L5.5A138.172A27.27A172.203L202.219A27.35L242.59A43.43A44.38L296.39A72.296L359.359A0.359L394.394A366.366A394.453L454.66L476.43A5.496L495.495L511.511A476.595L56.599L242.N.242L5.599A503.727A599.749L599.749A599.825L727.0A714.727L956.956A955.955A956.1043L1042.1043L0.0A1.1077A1.1119A1077.1144A1119.1168A1144.1186A1168.1202A1186.1A1077.1226A1.1253A1226.1275A1253.1299A1275.1317L1214.1214L1202.1202L1186.1186L1168.1168L1144.1144L1119.1119L1077.1077L1.1L1226.1226L1253.1253L1275.1275L1299.1299L1317.N.0A1.1168L0.0L2146.1144L0.0L2187.0L1299.0L1317.0L1214.0L1202.1186L0.1119L0.1077L0.1L0.1226L0.1253L0.1275L0.1186L1168.1168L1144.1144L1119.1119L1077.1077L1.1L1226.1226L1253.1253L1275.1275L1299.1299L1317.1317L1214.1214L1202.1202L1186.0L2487.0L2420.0L2349.0L2289.0L2236.0L2696.0L2649.0L2590.0L2.0L1076.0L2537.2696L1168.1168L2649.2649L1186.1186L2590.2590L1202.1202L2.2L1214.1214L1076.1076L1317.1317L2537.2537L1299.1299L2187.2187L1275.1275L2146.2146L1253.1253L2487.2487L1226.1226L2420.2420L1.1L2349.2349L1077.1077L2289.2289L1119.1119L2236.2236L1144.1144L2696.N.1168L2649.2649L1186.1186L2590.2590L1202.1202L2.2L1214.1214L1076.1076L1317.1317L2537.2537L1299.1299L2187.2187L1275.1275L2146.2146L1253.1253L2487.2487L1226.1226L2420.2420L1.1L2349.2349L1077.1077L2289.2289L1119.1119L2236.2236L1144.1144L2696.1168L2696.0A1
27-gon (none)
28-gon (from 14-gon)
https://sciencevsmagic.net/geo/#1A0.1L0.0L2.2A0.0A2.1L5.0L6.6A0.2A1.6L11.11A16.5L21.2L3.16A11.3L24.24A21.1A34.34A1.55L54.0A58.58A0.91L92.0L99.99L58.0A99.152L0.59L152.59A152.58A99.58L221.59L207.221L80.80A221.80L298.298A80.298L330.207A59.363A207.207L363.363L376.376A363.376L100.100L2.2L330.N.1A0.0A99.152A0.99A0.58A99.221A58.80A221.298A80.330A298.2A330.100A376.376A100.363A207.207A59.59A152.499L498.552L575.514L515.517L516.531L530.308L307.339L338.541L540.551L575.564L604.563L629.431L652.372L7.371L672.500L690.0L603.99L603.99L628.58L628.58L653.653L221.221L8.8L80.80L673.673L298.298L691.691L330.330L575.575L2.2L604.604L100.100L629.629L376.376L652.652L363.363L7.7L207.207L672.672L59.59L690.690L152.152L574.574L0
29-gon (none)
30-gon (from 15-gon)
https://sciencevsmagic.net/geo/#0A1.1A0.0L1.1L5.0L4.5A0.6L3.1A9.N.2L12.12L18.3L13.13L22.18L3.3L27.22L2.2L31.22L26.26L18.0A26.3L41.41L4.4L49.49L50.50L12.12L56.2L39.39L4.4L68.68L69.69L13.13L75.56L75.27L43.43L49.49L106.31L44.44L68.68L114.56L96.96L106.75L81.81L106.126L31.56L62.114L62.154L27.106L129.114L143.126L143.31L42.42L22.18L40.154L129.27L40.114L97.97L75.98L36.149L165.165L176.162L47.47L182.110L64.64L188.146L113.113L194.163L152.152L198.86L161.161L205.53L18.18L212.71L22.22L219.137L87.137L226.135L124.124L231.117L103.103L237.102L46.46L243.134L66.66L249.123L140.140L257.257L44.249L39.249L44.257L143.143L36.36L129.129L176.176L43.43L182.182L41.41L188.188L69.69L194.194L97.97L198.198L62.62L205.205L40.40L212.26L212.26L219.219L42.42L226.226L81.81L231.231L96.96L237.237L50.50L243.243L39
31-gon (none)
32-gon (from 16-gon)
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.2A1.1A2.4L5.1A7.1L11.11A7.11L17.N.0A1.17L7.17L8.7L21.8L27.0A17.27L35.21L34.8L33.33L32.2L31.31L8.8L43.43L19.19L56.31L7.7L65.65L25.25L78.34L66.66L89.35L58.58L99.78L92.92L113.111L108.108L2.2L125.125L32.32L1.1L143.101L47.47L149.149L89.143L82.82L165.33L169.169L178.125L69.69L190.190L99.178L160.165L56.101L160.113L33.114L106.106L222.105L90.90L236.150L57.57L250.130L145.145L264.203L129.129L278.189L211.211L292.149L192.192L306.127L208.208L320.205L187.187L223.191L68.68L237.166L80.80L251.175L164.164L265.180L116.107L168.168L297.180L279.167L182.182L307.178L121.121L321.321L108.108L307.307L2.297L293.2L293.293L169.169L279.279L82.82L265.265L36.36L251.251L8.8L237.237L25.25L223.223L69.69L320.320L194.194L306.306L1.1L292.292L135.135L278.278L47.47L264.264L19.19L250.250L7.7L236.236L58.58L222.222L92.92L321
33-gon
?
34-gon
?
35-gon
?
36-gon
?
37-gon (none)
38-gon
?
39-gon
?
40-gon
?
41-gon (none)
42-gon
?
43-gon (none)
44-gon
?
45-gon
?
46-gon
?
47-gon (none)
48-gon
?
49-gon
?
50-gon
?
51-gon
?
52-gon
?
53-gon
?
54-gon
?
55-gon (found a neat trick, but it didn’t work.)
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.3A0.0L3.3L9.9A3.9L11.11A9.11L14.14L4.15A1.1A15.31L32.1A35.0A54.54A1.71L72.0A75.N.0A24.2A112.0L10.126A0.137L138.1L54.54A35.117L174.174L192.192L162.N.0A1.205A2.218A205.2A205.250A2.234A218.267A250.282A234.302A267.344A302.2L205.2L250.250L267.267L302.302L344.344L360.360L316.316L282.282L234.234L218.218L205.N.2A0.6A218.692A6.701A692.708A701.716A205.205A716.736A205.756A736.771A756.783A771.791A783.2A791.809A2.825A809.832A825.183A832.849A183.250A849.872A250.886A872.894A886.904A894.8A904.267A8.930A267.942A930.951A942.961A951.969A302.302A969.986A302.1000A986.1008A1000.4A1008.1027A4.344A1027.1045A344.1057A1045.1066A1057.1076A1066.1086A1076.0A1.218A6.1106A218.1118A1106.1126A1118.1136A1126.1144A234.234A1144.1161A234.1175A1161.1185A1175.3A1185.1207A3.282A1207.1225A282.1238A1225.1249A1238.1261A1249.360A1086.1290A360.1308A1290.1A1308.1345A1.1356A1345.316A1356.16A316.316L16.16L1261.1261L1249.1249L1238.N.1238L1225.1225L282.282L1207.1207L3.3L1185.1185L1175.1175L1161.1161L234.234L1144.1144L1136.1136L1126.1126L1118.1118L1106.1106L218.218L6.6L692.692L701.701L708.708L716.716L205.205L736.736L756.756L771.771L783.783L791.791L2.2L809.809L825.825L832.832L183.183L849.849L250.250L872.872L886.886L894.894L904.904L8.8L267.267L930.930L942.942L951.951L961.961L969.969L302.302L986.1000L986.1008L1000.1008L4.1027L4.1027L344.1045L344.1045L1057.1066L1057.1066L1076.1076L1086.360L1086.1290L360.1308L1290.1L1308.1345L1.1356L1345.1356L316.16L316.16L1261.1261L1249.1249L1238.0A1
34 gon
https://sciencevsmagic.net/geo/#0L1.1A0.1L2.2A0.0A3.3A4.4A3.7L0.0L10.1L10.12A0.0A12.1L29.0A38.38A0.N.1L60.1L36.3L4.36A1.91A10.10A91.122L121.132A10.65A155.176A6.6A195.195A6.228L227.N.0A3.246L245.245A10.246L0.0L302.265L302.265L332.0A332.302L378.378L10.10L401.3L331.331L245.245L365.365L246.246L444.4L363.7L231.332L424.246L376.302L377.424L450.376L10.10L489.489L302.302L516.516L451.451L539.539L473.401L452.452L596.596L265.265L623.623L385.385L656.656L583.583L688.688L611.611L721.721L639.639L758.758L675.675L792.792L708.708L826.826L741.741L863.863L778.778L901.901L813.813L933.331L377.377L9.9L963.444L9.246L886.246L1033.1033L407.490L245.490L996.996L9.517L429.429L1111.1111L1094.963L886.10L997.863L864.864L1094.1094L1198.1198L987.987L1151.1151L517.331L624.1152L501.1260L1180.1260L1325.1325L1224.1224L1370.1359L528.1370L1136.1136L1437.1440L554
https://gist.github.com/mrflip/a973b1c60f4a38fc3277ddd57ce65b28
Scroll down on that website for 23, 25, 27, etc polygons by Doomslug682 here…
Circle pack 4 in 12 moves:
(spoiler incoming)
https://sciencevsmagic.net/geo/#0A1.1A0.2L3.1L0.0A4.1A4.4A0.0L17.17L21.17L22.17A22.21L33.21A33.1L17.17L41.41A45
(I rediscovered this after more than 2 years and actually did some more stuff in it including origin circle packing 3, origin circle packing 4, and pentagon in 13 moves (not in origin circle))
decagon in 19 moves, and it’s actually a pretty satisfying construction too
https://sciencevsmagic.net/geo/#0A1.1A0.2L3.0L1.2A0.8A1.1L11.4A13.0L22.0A22.29L30.30L28.29L24.28L25.29L53.1L28.1L60.30L58.30L51.51L42.43L24.24L71.71L70.70L68.58L35.33L25.25L82.82L75.75L22.22L89.89L52.89L71.68L22.22L59.106L82
44-gon
https://sciencevsmagic.net/geo/#0A1.1L0.0L2.1A0.3A0.0L3.3L9.9A3.9L11.11A9.11L14.14L4.15A1.1A15.31L32.1A35.0A54.54A1.71L72.0A75.N.0A24.2A112.0L10.126A0.137L138.1L54.54A35.117L174.174L192.192L162.N.0A1.205A2.218A205.2A205.250A2.234A218.267A250.282A234.302A267.344A302.2L205.2L250.250L267.267L302.302L344.344L360.360L316.316L282.282L234.234L218.218L205.N.0A229.344L666.302L369.267L353.250L309.2L229.205L259.293L218.329L234.282L664.316L0.360L0.666L0.369L0.353L0.309L0.0L766.0L698.0L229.0L668.0L787.0L807.0L829.0L853.0L259.0L893.0L873.0L293.0L718.0L329.0L742.0L664.664L766.766L665.665L668.668L667.667L787.787L666.666L807.807L369.369L829.829L353.353L853.853L309.309L873.873L229.229L893.893L259.259L698.698L293.293L718.718L329.329L742.664L742.874A766.0A775.1965L775.1988L1971.2097L0.0L2155.N.0L2154.0L1988.0L1965.0L1986.0L1976.0L1984.0L1974.0L1981.0L1972.0L1979.0L1970.0L1978.0L1987.0L1964.0L1985.0L1977.0L1983.0L1975.0L1982.0L1969.0L1973.0L1980.0L1971.0L775.1988L1986.2198L0.0L2236.2236L2265.1965L1976.2310L0.2310L2376.2376L2377.1986L1984.2424L0.2424L2482.2482L2483.1976L1974.2527L0.2527L2590.2590L2591.1984L1981.2637L0.2637L2704.2704L2705.1974L1972.2749L0.0L2812.2812L2813.1981L1979.2710L0.2710L1968.1972L1970.2928L0.2928L2996.2996L2997.775L1980.3037L0.3037L3110.3037L3111.1979L1978.3156L0.3156L3232.3232L3231.3231L1979.1979L2996.1972L2996.1972L1968.1968L1981.1981L2812.2812L1974.1974L2704.2704L1984.1984L2590.2590L1976.1976L2482.2482L1986.1986L2376.2376L1965.1965L2264.2264L1988.1988L2154.2154L775.775L3110.3110L1971.1971L3232.3232L1980.1980L2997.2997L1973.1973L1969.1969L1982.1982L2813.2813L1975.1975L2705.2705L1983.1983L2591.2591L1977.1977L2483.2483L1985.1985L2377.2377L1964.1964L2265.2265L1987.1987L2155.2155L1978.1978L3111.3111L1970.1970L3231
I have more
I wish there was a 3-dimensional version of this. (having challenges be polyhedra, circle packs into sphere packs, etc. https://www.youtube.com/watch?v=_QxrkEqOrWM This video will show all other polyhedra that will and won’t be in challenges, except for sphere packs. [polyhedra not in challenges will be saved if constructed])